The spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
The correct Answer is:(F2k)
12F2k
a. We hasve f=kx
→x=Fk
Acceleration =Fm
Time period T=2π√(displacement)/Acceleration)
=2π⎛⎜
⎜⎝√FkFm⎞⎟
⎟⎠=2√mk
Amplitude =max displacement
=Fk
The energy stored in the springh when the block passes through the equilibrium position
=12kx2=12(Fk)2
=12k(F2k2)=(F2k)
b. At the mean position P.E. is O.K.E. is
12kx2=12F2k
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
The springs shown in the figure are all unstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the blcok. Find the amplitude and the frequency of the motion of the block.
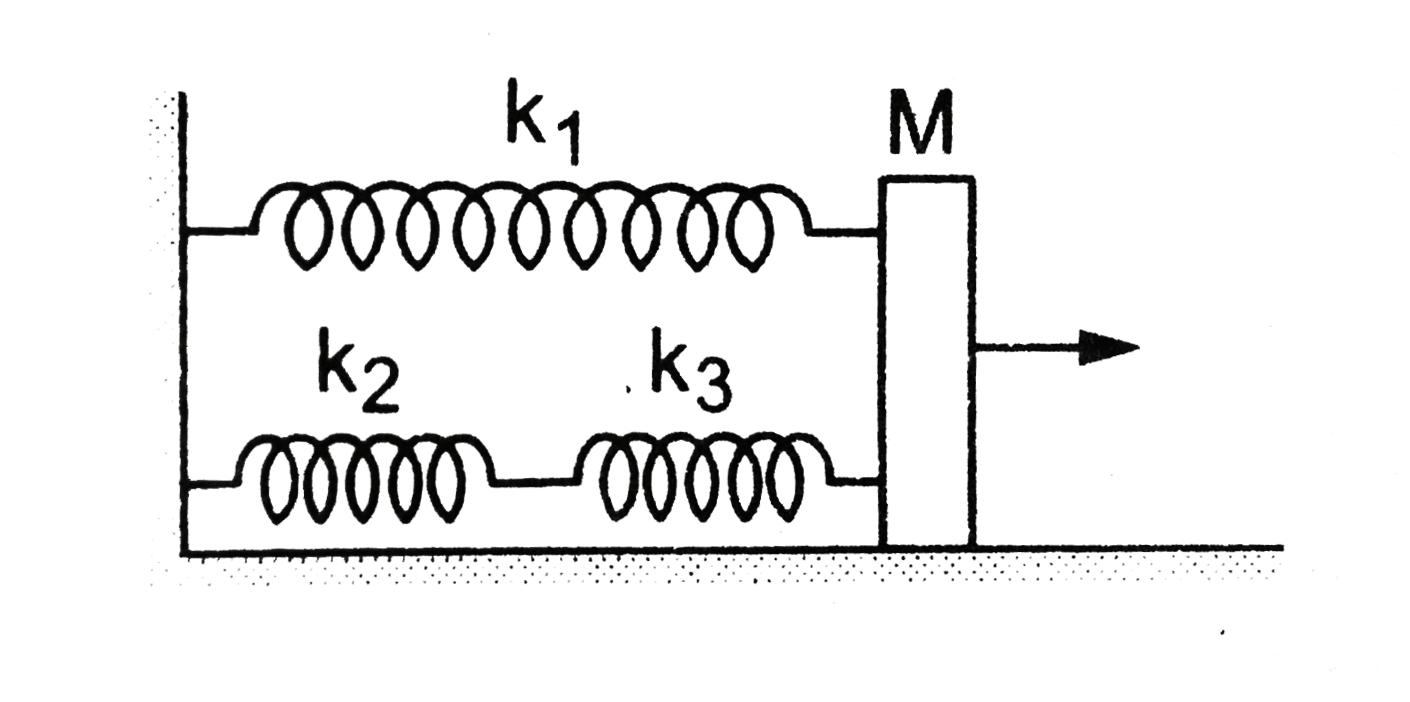
View SolutionA spring mass systeam is shown in figure, spring is initially unstretched. A man starts pulling the block with constant force F. Find
(a) The amplitude and the time period of motion of the block
(b) The K.E. of the block at mean position
(c) The energy stored in the spring when the block passes through the mean position
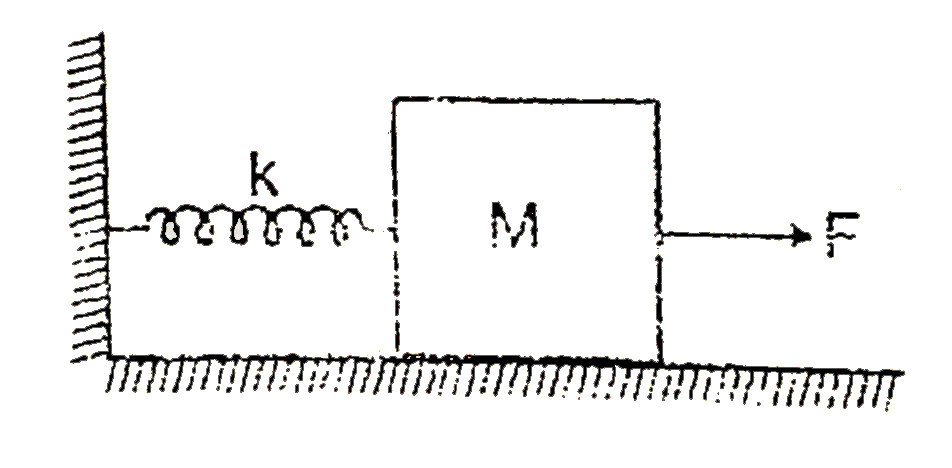
View Solution
Knowledge Check
The springs shown in the figure are all upstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the block.
 Athe amplitude of oscillation is (K2+K3)FK1K2+K2K3+K3K1Bthe oscillation frequency is 12π[K1K2+K2K3+K3K1M(K2+K3)]1/2Cthe amplitude of oscillation is 2(K2+K3)FK1K2+K2K3+K3K1Dthe oscillation frequency is 1π[K1K2+K2K3+K3K1M(K2+K3)]1/2
Athe amplitude of oscillation is (K2+K3)FK1K2+K2K3+K3K1Bthe oscillation frequency is 12π[K1K2+K2K3+K3K1M(K2+K3)]1/2Cthe amplitude of oscillation is 2(K2+K3)FK1K2+K2K3+K3K1Dthe oscillation frequency is 1π[K1K2+K2K3+K3K1M(K2+K3)]1/2
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.

View SolutionIn figure, k=100N/m,M=1kg and F=10N

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of 2m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA cord is used to vertically lower an initially stationary block of mass M at a constant downward acceleration of g/4. When the block has fallen a distance d, find (a) the work done by the cord's force on the block, (b) the work done by the graviational force on the block, (c) the kinitic energy of the block, and (d) the speed of the block.
View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionSpring mass system is shown in figure. Find the elastic potential energy stored in each spring when block is at its mean position. Also find the time period of vertical oscillations. The system is in vertical plane.

View Solution
