A particle of mass 1kg has velocity →v1=(2t)ˆi and another particle of mass 2kg has velocity →v2=(t2)ˆj
Column IColumn II(A)Netforce on centre of mass at 2 s(p)209unit(B)Velocity of centre of mass at 2 s(q)√68 unit(C)Displacement of centre of mass in 2s(r)√803unit(s)None
The correct Answer is:A →q, B →r, C →p
To solve the problem step-by-step, we will analyze the motion of two particles and calculate the required quantities: net force on the center of mass, velocity of the center of mass, and displacement of the center of mass.
Step 1: Calculate the acceleration of each particle
1. For Particle 1 (mass = 1 kg):
- Given velocity: →v1=(2t)^i
- Acceleration →a1=d→v1dt=ddt(2t^i)=2^i (m/s²)
2. For Particle 2 (mass = 2 kg):
- Given velocity: →v2=(t2)^j
- Acceleration →a2=d→v2dt=ddt(t2^j)=2t^j (m/s²)
Step 2: Calculate the acceleration of the center of mass
- Total mass M=m1+m2=1kg+2kg=3kg
- Acceleration of the center of mass →aCM is given by:
→aCM=m1→a1+m2→a2M
Substituting the values:
→aCM=1⋅(2^i)+2⋅(2t^j)3=2^i+4t^j3=23^i+4t3^j
Step 3: Calculate the net force on the center of mass at t=2s
- Substitute t=2:
→aCM=23^i+83^j
- Net force →FCM=M→aCM:
→FCM=3(23^i+83^j)=2^i+8^j
Step 4: Calculate the magnitude of the net force
|→FCM|=√(2)2+(8)2=√4+64=√68N
Step 5: Calculate the velocity of the center of mass at t=2s
- Velocity of the center of mass →vCM is given by:
→vCM=m1→v1+m2→v2M
Substituting the values:
- For t=2:
→v1=4^i,→v2=4^j
→vCM=1⋅(4^i)+2⋅(4^j)3=4^i+8^j3=43^i+83^j
Step 6: Calculate the magnitude of the velocity of the center of mass
|→vCM|=√(43)2+(83)2=√169+649=√809=√803m/s
Step 7: Calculate the displacement of the center of mass in 2 seconds
- Displacement →sCM can be calculated by integrating the velocity:
→sCM=∫20→vCMdt
Using the expression for →vCM:
→sCM=∫20(23t^i+t23^j)dt
Calculating the integrals:
→sCM=(23⋅t22^i+13⋅t33^j)20=(23⋅22^i+13⋅83^j)=(83^i+89^j)
Step 8: Calculate the magnitude of the displacement
|→sCM|=√(83)2+(89)2=√649+6481=√576+6481=√64081=8√109
Final Answers
- Net force on center of mass at 2 s: √68N
- Velocity of center of mass at 2 s: √803m/s
- Displacement of center of mass in 2s: 209units
1. For Particle 1 (mass = 1 kg):
- Given velocity: →v1=(2t)^i
- Acceleration →a1=d→v1dt=ddt(2t^i)=2^i (m/s²)
- Given velocity: →v2=(t2)^j
- Acceleration →a2=d→v2dt=ddt(t2^j)=2t^j (m/s²)
- Total mass M=m1+m2=1kg+2kg=3kg
- Acceleration of the center of mass →aCM is given by:
→aCM=m1→a1+m2→a2M
Substituting the values:
→aCM=1⋅(2^i)+2⋅(2t^j)3=2^i+4t^j3=23^i+4t3^j
- Substitute t=2:
→aCM=23^i+83^j
- Net force →FCM=M→aCM:
→FCM=3(23^i+83^j)=2^i+8^j
|→FCM|=√(2)2+(8)2=√4+64=√68N
- Velocity of the center of mass →vCM is given by:
→vCM=m1→v1+m2→v2M
Substituting the values:
- For t=2:
→v1=4^i,→v2=4^j
→vCM=1⋅(4^i)+2⋅(4^j)3=4^i+8^j3=43^i+83^j
|→vCM|=√(43)2+(83)2=√169+649=√809=√803m/s
- Displacement →sCM can be calculated by integrating the velocity:
→sCM=∫20→vCMdt
Using the expression for →vCM:
→sCM=∫20(23t^i+t23^j)dt
Calculating the integrals:
→sCM=(23⋅t22^i+13⋅t33^j)20=(23⋅22^i+13⋅83^j)=(83^i+89^j)
|→sCM|=√(83)2+(89)2=√649+6481=√576+6481=√64081=8√109
- Net force on center of mass at 2 s: √68N
- Velocity of center of mass at 2 s: √803m/s
- Displacement of center of mass in 2s: 209units
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
If net force on a system of particles is zero. Then
Column IColumn II(A)Acceleration of centre of mass(p)Constant(B)Velocity of centre of mass(q)Zero(C)Momentum of centre of mass(r)May be zero(D)Velocity of an individual particle of the system(s)May be constant
View SolutionThe particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
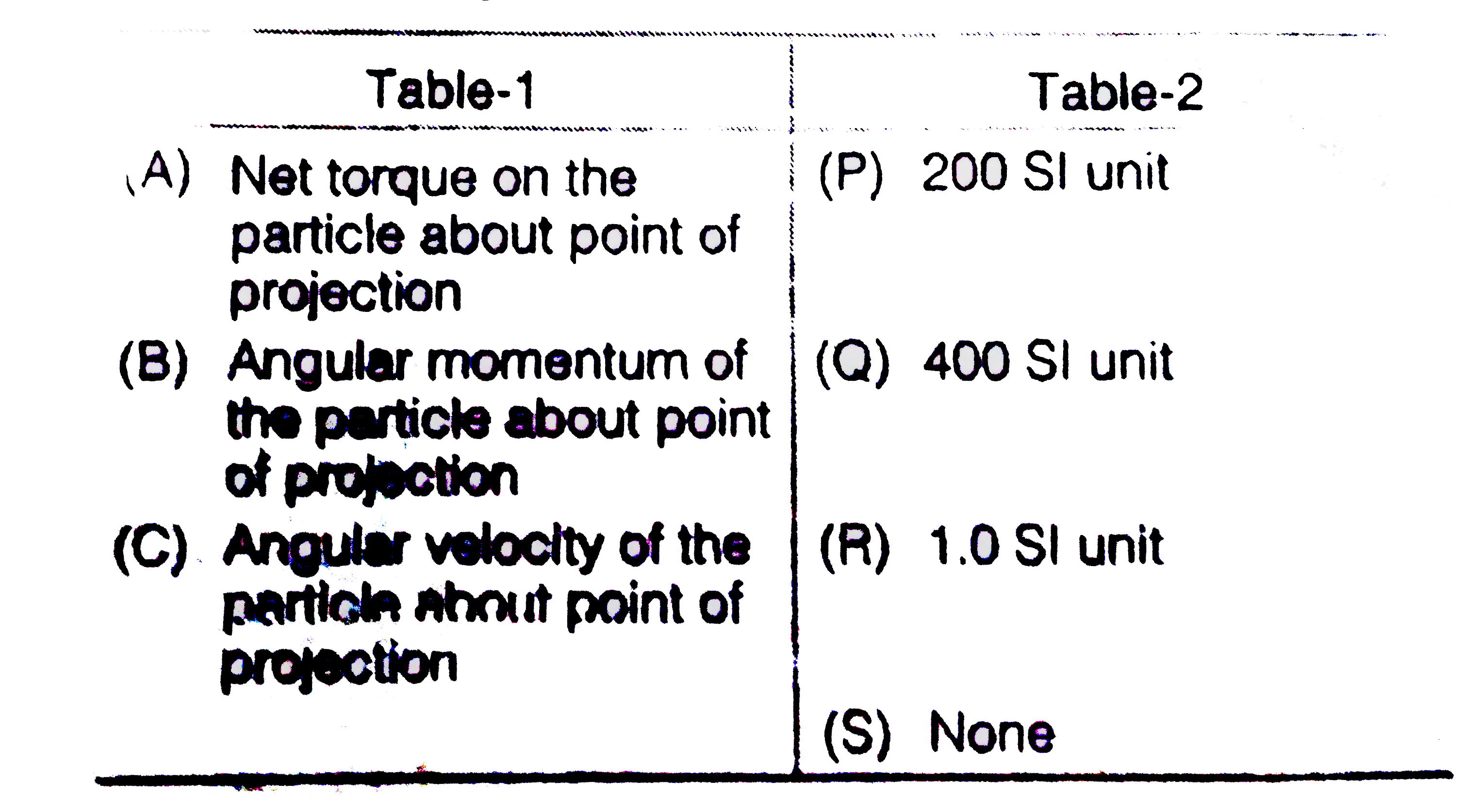
View SolutionIn the s-t equation (s=10+20t−5t2) match the following columns.
∣∣ ∣ ∣ ∣ ∣ ∣∣Column IColumn II(A)Distancec travelled in 3s(p)−20 units(B)Displacement 1 s(q)15 units(C)Initial acceleration(r)25 units(D)Velocity at 4 s(s)−10 units∣∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionA particle of mass 2kg is moving with velocity →v0=(2ˆi−3ˆj)m/s in free space. Find its velocity 3s after a constant force →F=(3ˆi+4ˆj)N starts acting on it.
View SolutionA 2.0 kg particle has a velocity of →v1=(2.0ˆi−3.0ˆj)m/s, and a 3.0kg particle has a velocity →v2=(1.0ˆi+6.0ˆj)m/s. How fast is the center of mass of the particle system moving?
View SolutionTwo particles of equal mass have coordinates (2m,4m,6m) and (6m,2m,8m). Of these one particle has a velocity v1=(2i)ms−1 and another particle has a velocity v2=(2j)ms−1 at time t=0. The coordinate of their center of mass at time t=1s will be
View SolutionA particle of mass 1 kg is projected upwards with velocity 60ms−1. Another particle of mass 2kg is just dropped from a certain height. After 2s, match the following.
[Take, g =10ms−2]
column1column2Accelertion of CMP ZeroB Velocity of CMQ 10 SI unitC Displacement of CMR 20 SI unit-S None
View SolutionTwo particles of masses m and 3m approach each other with different velocities. After collision, the particle of mass m has velocity →v in their centre of mass frame. Velocity of particle of mass 3m in the centre of mass frame is
View SolutionA particle is moving with speed 6m/s along the direction of →A=2ˆi+2ˆj−ˆk, then its velocity is :
View SolutionA particle of mass 'm' moving with a velocity (3ˆi+2ˆj)m/s collides with stationary mass 'M' and finally 'm' moves with a velocity (−2ˆi+ˆj)m/s if mM=113 the velocity of the M after collision is?
View Solution
