If net force on a system of particles is zero. Then
Column IColumn II(A)Acceleration of centre of mass(p)Constant(B)Velocity of centre of mass(q)Zero(C)Momentum of centre of mass(r)May be zero(D)Velocity of an individual particle of the system(s)May be constant
The correct Answer is:A -q, B-r, Crr,D→s
To solve the question, we need to analyze the implications of having a net force of zero on a system of particles. Let's break it down step by step.
Step 1: Understanding the Implication of Zero Net Force
When the net force acting on a system of particles is zero, according to Newton's second law, we have:
Fnet=m⋅acm
where acm is the acceleration of the center of mass. If Fnet=0, then:
acm=0
This means that the acceleration of the center of mass is constant, specifically zero.
Hint: Remember that zero net force implies no change in velocity, hence zero acceleration.
Step 2: Analyzing the Velocity of the Center of Mass
Since the acceleration of the center of mass is zero, it follows that the velocity of the center of mass must be constant. This means that:
- The velocity of the center of mass can be a constant value (which could be non-zero) or it could be zero.
Hint: Consider that constant velocity means no acceleration; thus, the center of mass maintains its velocity.
Step 3: Analyzing the Momentum of the Center of Mass
The momentum of the center of mass Pcm is given by:
Pcm=m⋅vcm
Since the velocity of the center of mass is constant, the momentum of the center of mass is also constant. However, if the center of mass is at rest (velocity is zero), then the momentum can also be zero. Thus:
- The momentum of the center of mass is constant and may be zero.
Hint: Momentum is directly related to velocity; if velocity is constant, momentum is constant too.
Step 4: Velocity of Individual Particles
The velocities of individual particles in the system can vary. While the center of mass has a constant velocity, individual particles can have different velocities that may change. Therefore:
- The velocity of an individual particle may be constant or may change, depending on the system.
Hint: Individual particle motion can be complex, even if the center of mass moves uniformly.
Conclusion
Now, we can match the items from Column I with Column II based on our analysis:
- (A) Acceleration of center of mass → (p) Constant (since acm=0)
- (B) Velocity of center of mass → (q) Constant (may be zero)
- (C) Momentum of center of mass → (r) May be zero (but constant)
- (D) Velocity of an individual particle of the system → (s) May be constant (depends on the particle)
Final Matching:
- A → p (Constant)
- B → q (Zero or Constant)
- C → r (May be Zero)
- D → s (May be Constant)
When the net force acting on a system of particles is zero, according to Newton's second law, we have:
Fnet=m⋅acm
where acm is the acceleration of the center of mass. If Fnet=0, then:
acm=0
This means that the acceleration of the center of mass is constant, specifically zero.
Since the acceleration of the center of mass is zero, it follows that the velocity of the center of mass must be constant. This means that:
- The velocity of the center of mass can be a constant value (which could be non-zero) or it could be zero.
The momentum of the center of mass Pcm is given by:
Pcm=m⋅vcm
Since the velocity of the center of mass is constant, the momentum of the center of mass is also constant. However, if the center of mass is at rest (velocity is zero), then the momentum can also be zero. Thus:
- The momentum of the center of mass is constant and may be zero.
The velocities of individual particles in the system can vary. While the center of mass has a constant velocity, individual particles can have different velocities that may change. Therefore:
- The velocity of an individual particle may be constant or may change, depending on the system.
Now, we can match the items from Column I with Column II based on our analysis:
- (B) Velocity of center of mass → (q) Constant (may be zero)
- (C) Momentum of center of mass → (r) May be zero (but constant)
- (D) Velocity of an individual particle of the system → (s) May be constant (depends on the particle)
- A → p (Constant)
- B → q (Zero or Constant)
- C → r (May be Zero)
- D → s (May be Constant)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A particle of mass 1kg has velocity →v1=(2t)ˆi and another particle of mass 2kg has velocity →v2=(t2)ˆj
Column IColumn II(A)Netforce on centre of mass at 2 s(p)209unit(B)Velocity of centre of mass at 2 s(q)√68 unit(C)Displacement of centre of mass in 2s(r)√803unit(s)None
View SolutionThe centre of mass of a system of particles is at the origin. It follows that:
View SolutionIf the net external forces acting on the system oif particles is zero, then which of the following may vary?
View SolutionColumn IColumn II(A)Dimensional variable(p)π(B)Dimensionless variable(q)Force(C)Dimensional constant(r)Angle(D)Dimensionless constant(s)Gravitational constant
View SolutionA particle of mass m, kinetic energy K and momentum p collides head on elastically with another particle of mass 2m at rest. After collision, :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9(t)None
View SolutionA balloon rises up with constant net acceleration of 10m/s2. After 2 s a particle drops from the balloon. After further 2 s match the following : (Takeg=10m/s2)
Column IColumn II(A)Height of perticle from ground(p)Zero(B)Speed of particle(q)10SIunits(C)Displacement of Particle(r)40SIunits(D)Acceleration of particle(s)20SIunits
View SolutionIf some charge is given to a conducting object of any shape, then match the following columns, under electrostatic condition
Column IColumn II(A)→E at a point within conducting material(p)Must be zero(B)→Eat a point outside the material (q)May be Zero(C)→Eat a point in a cavity having no charge(r)May be uniform but not zero(D)→Eat a point in the cavity having some charge(s)May be non-uniform(t)Cannot predict
View SolutionIn a two block system in figure match the following.
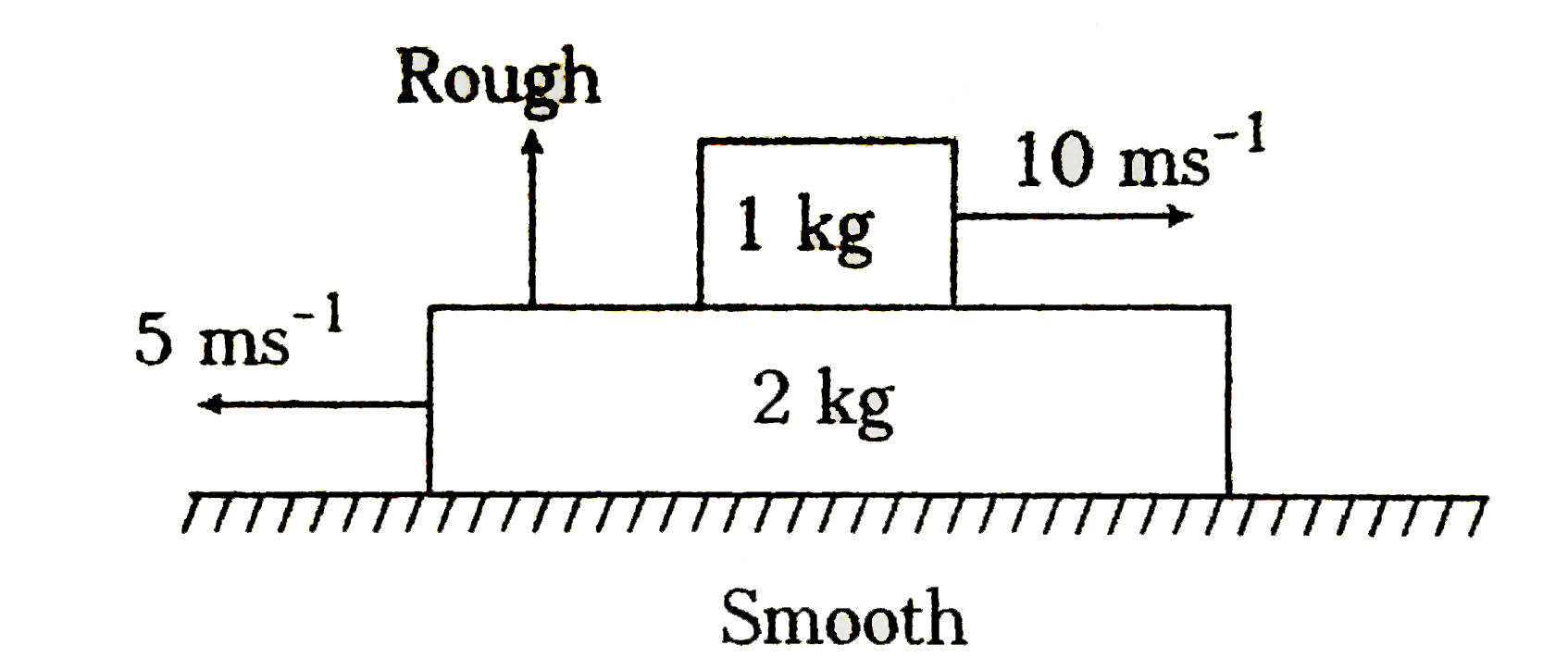 Column1Column2A Velocity of center of massP Keep on changing all the timeB Momentum of center of massQ First decreases then become zeroC Momentum of 1kg blockR ZeroD Kinetic energy of 2kg blockS Constant
Column1Column2A Velocity of center of massP Keep on changing all the timeB Momentum of center of massQ First decreases then become zeroC Momentum of 1kg blockR ZeroD Kinetic energy of 2kg blockS Constant
View SolutionMatch the following columns.
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣Column IColumn II(A)Constant positive acceleration(p)Speed may increase(B)Constant negative acceleration(q)Speed may decrease(C)Constant displacement(r)Speed is zero(D)Constant slope of a-t graph(s)Speed must increase(t)Speed must decrease∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionA nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to bev0anda0 at an instant t. It is possible that:
View Solution
