A particle of mass 1 kg is projected upwards with velocity 60 m/s. Another particle of mass 2 kg is just deopper from a certain height. After 2 kg is just of the particles have colliided with ground, match the following [ Take g= 10 m/s2]
To solve the problem step by step, we will analyze the motion of both particles and find their velocities after 2 seconds before determining the center of mass velocity.
Step 1: Determine the velocity of the 2 kg particle after 2 seconds.
The 2 kg particle is dropped from a certain height. We can use the equation of motion to find its velocity after 2 seconds.
Formula:
v=u+gt
Where:
- u=0 (initial velocity, since it is dropped)
- g=10m/s2 (acceleration due to gravity)
- t=2s
Calculation:
v=0+(10m/s2)(2s)=20m/s
Step 2: Determine the velocity of the 1 kg particle after 2 seconds.
The 1 kg particle is projected upwards with an initial velocity of 60 m/s. We will also use the equation of motion to find its velocity after 2 seconds.
Formula:
v=u−gt
Where:
- u=60m/s (initial velocity)
- g=10m/s2
- t=2s
Calculation:
v=60m/s−(10m/s2)(2s)=60m/s−20m/s=40m/s
Step 3: Calculate the center of mass velocity after 2 seconds.
Now, we will find the velocity of the center of mass of the system consisting of both particles.
Formula:
Vcm=m1v1+m2v2m1+m2
Where:
- m1=1kg
- v1=40m/s (upward, positive direction)
- m2=2kg
- v2=−20m/s (downward, negative direction)
Calculation:
Vcm=(1kg)(40m/s)+(2kg)(−20m/s)1kg+2kg
Vcm=40−403=03=0m/s
Conclusion
After 2 seconds, the velocity of the center of mass of the system is 0 m/s.
---
v=u+gt
- u=0 (initial velocity, since it is dropped)
- g=10m/s2 (acceleration due to gravity)
- t=2s
v=0+(10m/s2)(2s)=20m/s
v=u−gt
- u=60m/s (initial velocity)
- g=10m/s2
- t=2s
v=60m/s−(10m/s2)(2s)=60m/s−20m/s=40m/s
Vcm=m1v1+m2v2m1+m2
- m1=1kg
- v1=40m/s (upward, positive direction)
- m2=2kg
- v2=−20m/s (downward, negative direction)
Vcm=(1kg)(40m/s)+(2kg)(−20m/s)1kg+2kg
Vcm=40−403=03=0m/s
Similar Questions
A particle of mass 1 kg is projected upwards with velocity 60ms−1. Another particle of mass 2kg is just dropped from a certain height. After 2s, match the following.
[Take, g =10ms−2]
column1column2Accelertion of CMP ZeroB Velocity of CMQ 10 SI unitC Displacement of CMR 20 SI unit-S None
View SolutionA particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionThe particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
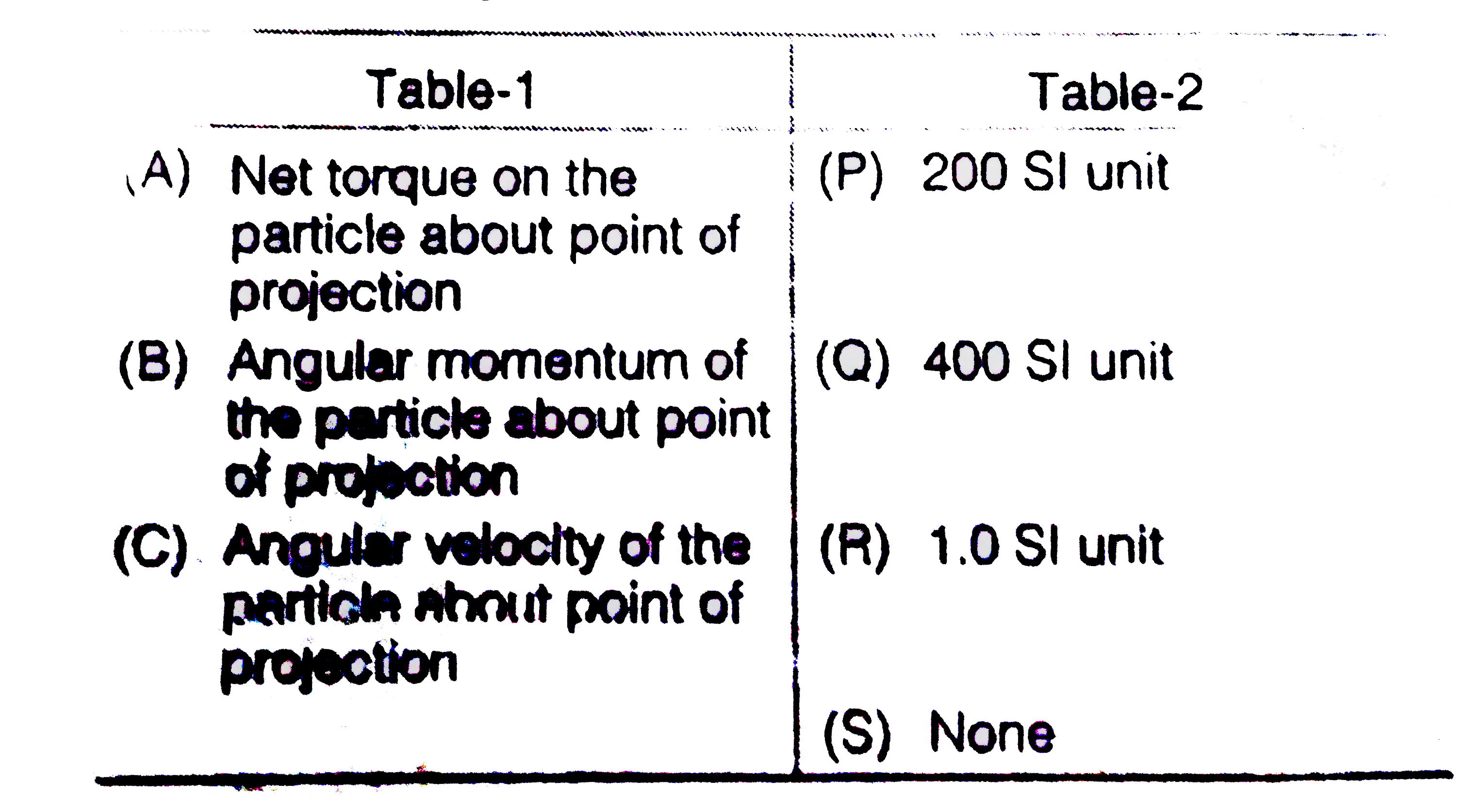
View SolutionA particle is projected from ground with velocity 20(√2)m/s at 45∘. At what time particle is at height 15 m from ground? (g=10m/s2)
View SolutionA body of mass 2 kg is dropped from rest from a height 20 m from the surface of Earth. The body hits the ground with velocity 10 m/s, then work done: (g=10m/s2)
View SolutionA particle is projected upwards with velocity 40m/s. Taking the value of g=10m/s2 and upward direction as positive, plot a-t,v-t and s-t graphs of the particle from the starting point till it further strikes the ground.
View SolutionA body of mass 2kg is projected upward from the surface of the ground at t=0 with a velocity of 20m/s. One second later a body B, also of mass 2kg, is dropped from a height of 20m. If they collide elastically, then velocities just after collision are :-
View SolutionA particle of mass 2 kg is projected vertically upward with a velocity of 20 m/s. It attains maximum height of 17 m. The loss in mechanical energy due to air drag is (g=10ms−2)
View SolutionComprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
The centre of mass of the two particles is moving in a straight line for which equation is :
View Solution
