Comprehension # 5
One particle of mass is moving along positive x-axis with velocity . Another particle of mass is moving along y-axis with . At time mass is at and at plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
The centre of mass of the two particles is moving in a straight line for which equation is :
y=x+2
y=4x+2
y=2x-4
y=2x+4
To find the equation of the line along which the center of mass of the two particles is moving, we can follow these steps:
Step 1: Identify the masses and their velocities
- Mass of particle 1, m1=1kg
- Velocity of particle 1, →v1=3m/s^i (moving along the x-axis)
- Mass of particle 2, m2=2kg
- Velocity of particle 2, →v2=6m/s^j (moving along the y-axis)
Step 2: Calculate the velocity of the center of mass
The velocity of the center of mass →vcm is given by the formula:
→vcm=m1→v1+m2→v2m1+m2
Substituting the values:
→vcm=1⋅3^i+2⋅6^j1+2=3^i+12^j3=1^i+4^j
Step 3: Determine the slope of the center of mass motion
The velocity vector →vcm=1^i+4^j indicates that the center of mass moves with a velocity of 1 in the x-direction and 4 in the y-direction. The slope m of the line can be calculated as:
m=vyvx=41=4
Step 4: Find the initial position of the center of mass
The initial positions of the particles are:
- Particle 1: (3,0)
- Particle 2: (0,9)
The position of the center of mass →Rcm is given by:
→Rcm=m1→r1+m2→r2m1+m2
Substituting the values:
→Rcm=1⋅(3,0)+2⋅(0,9)1+2=(3,0)+(0,18)3=(3,18)3=(1,6)
Step 5: Write the equation of the line
Using the point-slope form of the equation of a line:
y−y1=m(x−x1)
Where (x1,y1)=(1,6) and m=4:
y−6=4(x−1)
Expanding this:
y−6=4x−4⟹y=4x+2
Final Answer
The equation of the line along which the center of mass is moving is:
y=4x+2
- Mass of particle 1, m1=1kg
- Velocity of particle 1, →v1=3m/s^i (moving along the x-axis)
- Mass of particle 2, m2=2kg
- Velocity of particle 2, →v2=6m/s^j (moving along the y-axis)
The velocity of the center of mass →vcm is given by the formula:
→vcm=m1→v1+m2→v2m1+m2
Substituting the values:
→vcm=1⋅3^i+2⋅6^j1+2=3^i+12^j3=1^i+4^j
The velocity vector →vcm=1^i+4^j indicates that the center of mass moves with a velocity of 1 in the x-direction and 4 in the y-direction. The slope m of the line can be calculated as:
m=vyvx=41=4
The initial positions of the particles are:
- Particle 1: (3,0)
- Particle 2: (0,9)
→Rcm=m1→r1+m2→r2m1+m2
Substituting the values:
→Rcm=1⋅(3,0)+2⋅(0,9)1+2=(3,0)+(0,18)3=(3,18)3=(1,6)
Using the point-slope form of the equation of a line:
y−y1=m(x−x1)
Where (x1,y1)=(1,6) and m=4:
y−6=4(x−1)
Expanding this:
y−6=4x−4⟹y=4x+2
The equation of the line along which the center of mass is moving is:
y=4x+2
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:More a than one option is Correct
Explore 1 Video
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Medical entrances gallery
Explore 27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
Similar Questions
Comprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
If both the particles have the same value of coefficient of friction μ=0.2. The centre of mass will stop at time t= ..........s :-
View SolutionComprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is rough for question, if cofficient of friction is 0.2 in both axis)
Co-ordinates of center of mass where it will stop finally are :-
View SolutionThe position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
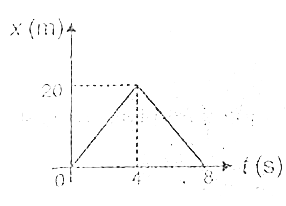
View SolutionA particle of mass m1=4kg moving at 6ˆims−1 collides perfectly elastically with a particle of mass m2=2 moving at 3ˆims−1
View SolutionA body of mass m=3.513kg is moving along the x-axis with a speed of 5.00ms−1. The magnetude of its momentum is recorded as
View SolutionA body of mass m=3.513kg is moving along the x-axis with a speed of 5.00ms−1. The magnetude of its momentum is recorded as
View SolutionA block of mass 1kg is at x=10m and moving towards negative x−aξs with velocity 6m/s. Another block of mass 2kg is at x=12m and moving towards positive x−axis with velocity 4m/s at the same instant. Find position of their centre of mass after 2s.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionA particle of mass 1 kg is projected upwards with velocity 60 m/s. Another particle of mass 2 kg is just deopper from a certain height. After 2 kg is just of the particles have colliided with ground, match the following [ Take g= 10 m/s2]
View Solution