A particle of mass 10−2kg is moving along the positive x axis under the influence of a force F(x)=−K/(2x2) where K=10−2Nm2. At time t=0 it is at x=1.0m and its velocity is v=0.
(a) Find its velocity when it reaches x=0.50m.
(b) Find the time at which it reaches x=0.25m.
(a) As F=ma=mdvdt
=mvdvdx[asdvdt=dvdx.dxdt=vdvdx]
and according to given problem F=−K/(2x2), so
mvdvdx=−k2x2.
i.e., ∫v0dv=1m∫x1−K2x2dx
Or v2=km(1x−1)=10−210−2(1x−1)=(1x−1)...........(i)
So, for x=0.5m, v2=(2−1), i.e., v=±1 m/s
And as here the force is opposite to displacment and particle starts moving from x=1 towards the origin i.e., with increase in time, xdecreases, i.e., v(=-dx/dt) will be negative,
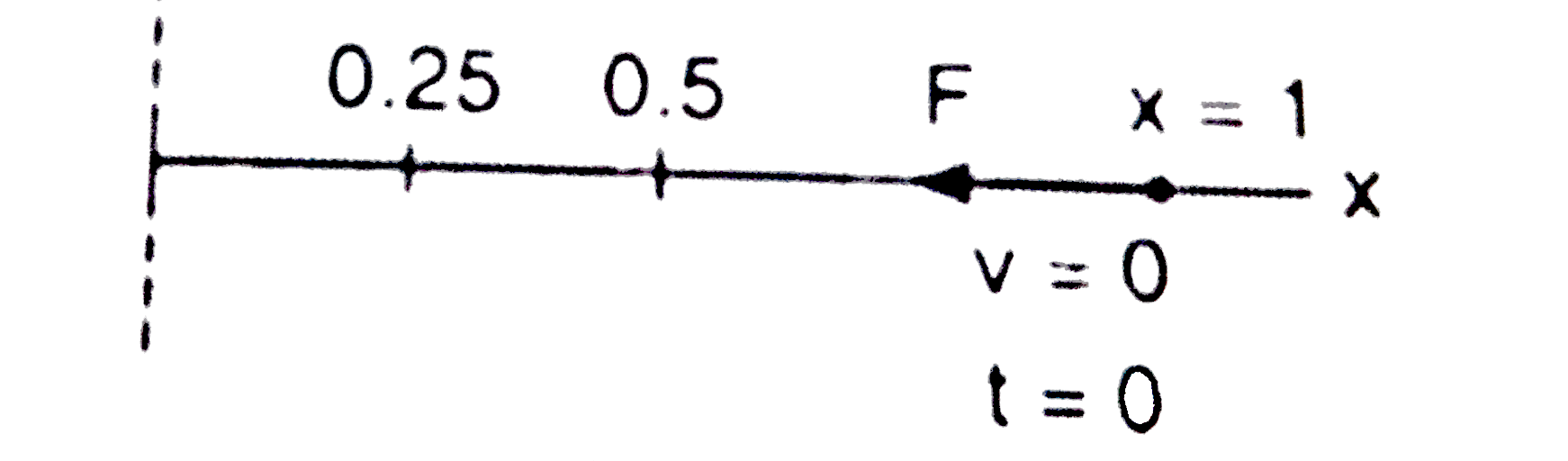
So, v=−1(m/s)
(b) As from Eqn. (i)
v=(1−x)x,i.e.,−dxdt=(1−x)x [as here v=−dxdt]
So, ∫t0dt=−∫0.251x(1−x)dx
To integrate the above expression let x=sin2θ so that =2sinθcosθdθ and hence
t=−∫π/6π/2[sin2θ1−sin2θ]1/22sinθcosθdthη
=−∫π/6π/22sin2dthη
i.e., t=−∫π/6π/2(1−cos2θ)dθ
=[θ−12sin2θ]π/2π/6=(π3+√3r)s.
Topper's Solved these Questions
Similar Questions
A particle moves along the X-axis from x=0→x=5m under the influence of a force given by F=(7−2x+3x2). Find the work done in the process.
View SolutionA particle moves along the X-axis from x=0 to x=5 m under the influence of a force given by F=7−2x+3x2. Find the work done in the process.
View Solution
Knowledge Check
A particle moves along the X-axis x=0 to x=5 m under the influence of a force given by F=10−2x+3x2. Work done in the process is
A70 unitsB270 unitsC35 unitsD150 unitsA particle moves along X-axis from x=0 to x=1 m under the influence of a force given by F=3x2+2x−10. Work done in the process is
A+4JB−4JC+8JD−8JA particle A of mass 10/7kg is moving in the positive direction of x−aξs. At initial position x=0, its velocity is 1ms−1, then its velocity at x=10m is (use the graph given)
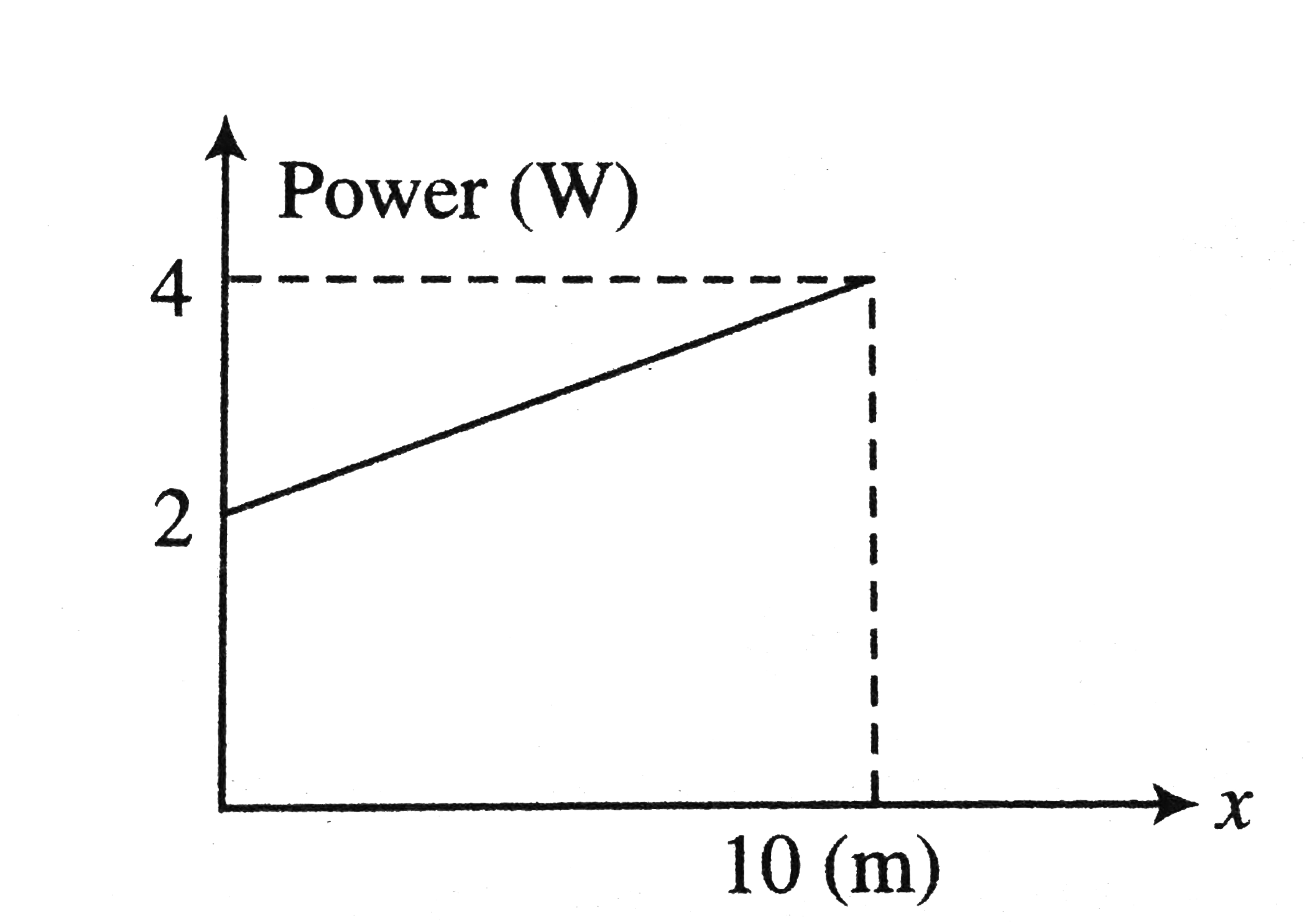 A(a) 4ms−1B(b) 2ms−1C(c) 3√2ms−1D(d) 1003ms−1
A(a) 4ms−1B(b) 2ms−1C(c) 3√2ms−1D(d) 1003ms−1
A particle moves along x-axis from x=0 to x=2 m under the influence of a force F (in N) given by F=3x2+2x−5. Calculate the work done
View SolutionA particle starts moving along the x-axis from t=0, its position varying with time as x=2t3−3t2+1.
a. At what time instants is its velocity zero?
b. What is the velocity when it passes through the origin?
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by
F=7−2x+3x2. The instantaneous power applied to the particle is.
View SolutionA body of mass m, moving along the positive x direction is subjected to a resistive force F=Kv2 (where K is a constant and v the particle n velocity). If m=10kgv=10m/s at t=0, and K=2N(m/s)−2 the velocity when t=2s is:
View SolutionA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View Solution
