Question

In an experiment for measuring 'g', a body is thrown vertically up in an evacuated tube and allowed to come back. If ${\displaystyle \Delta T_L}$ is the time interval between the two passages of the object across a lower level and ${\displaystyle \Delta T_H}$ the time interval between two passages across an upper level and H the distance between two levels as shown in Fig. 5.70 show that:
${\displaystyle g=\frac{8H}{\Delta T_L^2-\Delta T_H^2}}$

Explanation

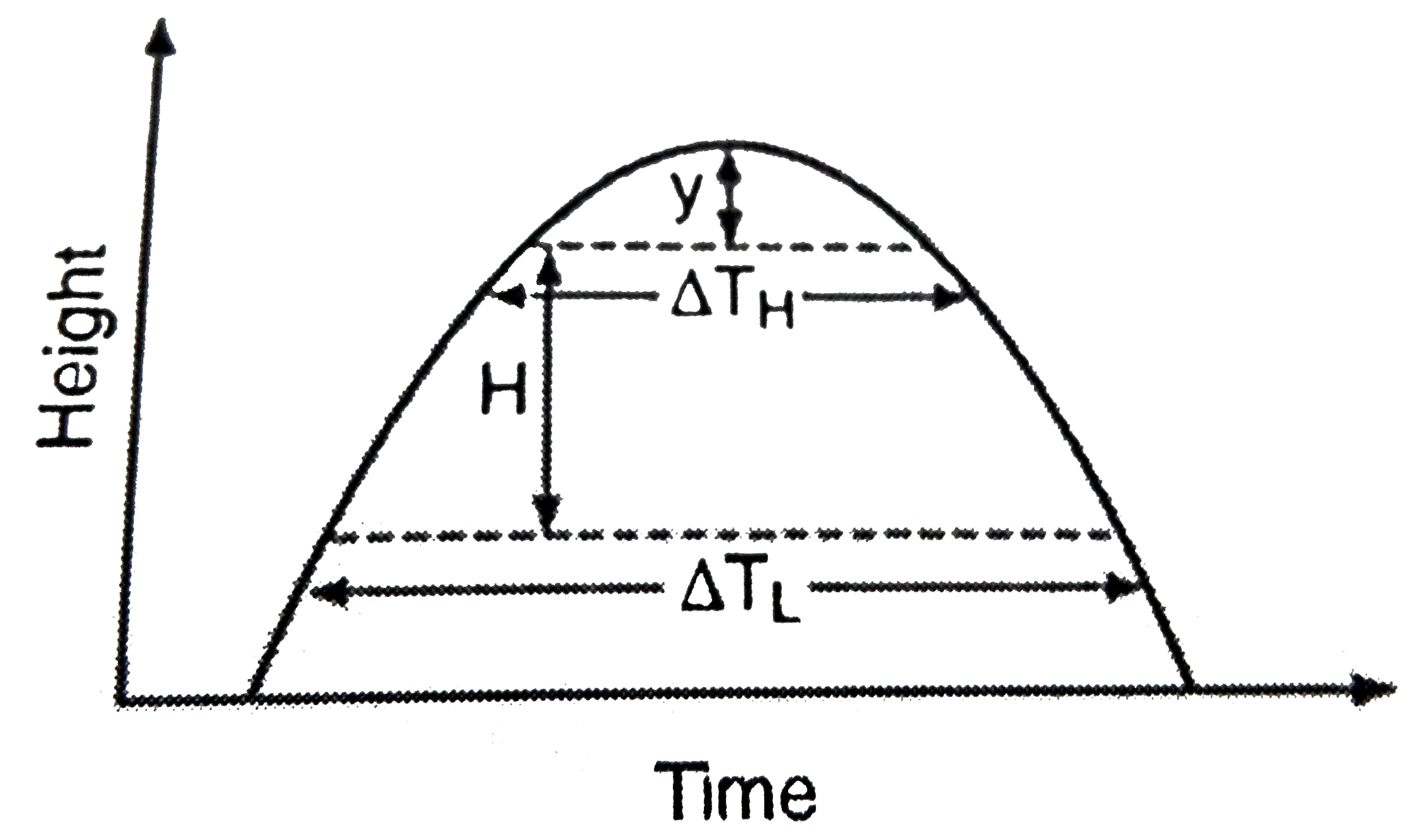
Time taken by a body to go up and come down a height h is giving by t=2, `sqrt((2h//g))sqrt((8h//g))`. So , if y is the height of highest point above higher level, time taken to go up and come down `DeltaT_(H)=sqrt((8y//g))` while for lower level
`DeltaT_(L)=sqrt([8(y+h)//g])`.
`therefore DeltaT_(L)^(2)-DeltaT_(H)^(2)=(8(y+H))/(g)-(8y)/(g)=(8H)/(g)`
or `g=(8H)/((DeltaT_(L)^(2)-DeltaT_(H)^(2)))`