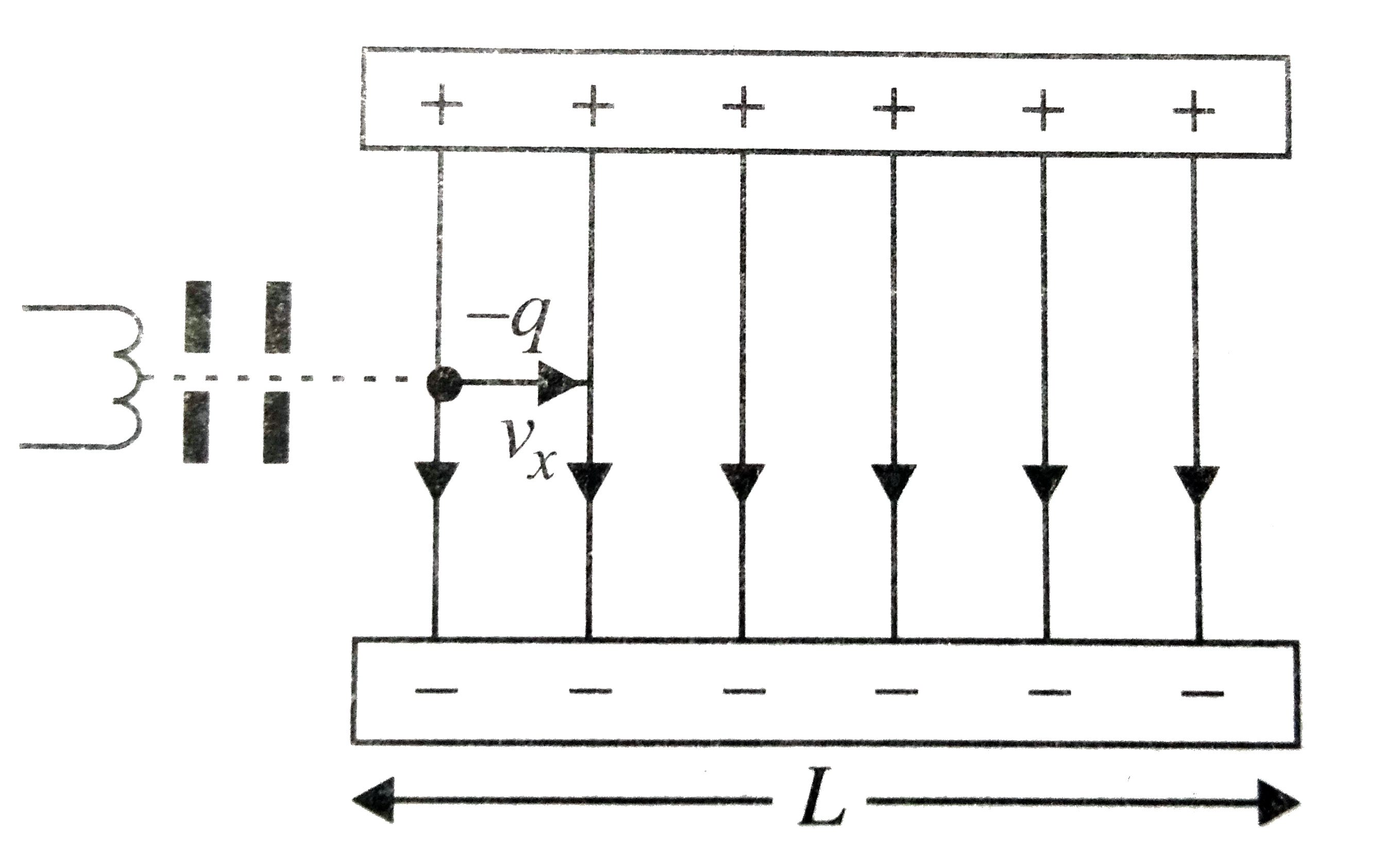
A particle of mass m and charge (-q) enters the region between the two charged plates initially moving along x-axis with speed vx (like particle 1 in Figure). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL22mv2x. Compare this motion with motion of a projectile in gravitational field. 
Charge on a particle of mass m = − q
Velocity of the particle = VX
Length of the plates = L
Magnitude of the uniform electric field between the plates = E
Mechanical force, F = Mass (m) × Acceleration (a)
a=Fm
However, electric force, F=qE
Therefore, acceleration, a=qEm ...(1)
Time taken by the particle to cross the fields of length L is given by,
t=Length of the plateVelocity of the particle=Lvx ...(2)
In the vertical direction, initial velocity, u = 0
According to the third equation of motion, vertical deflection s of the particle can be obtained as,
s=ut+12at2
s=0+12(qEm)(Lvx)2
s=qEL22mv2x ...(3)
Hence, vertical deflection of the particle at the far edge of the plate is
qEL2/(2mv2x). This is similar to the motion of horizontal projectiles under gravity.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERTCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE
34 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERTCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
37 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
17 Videos
Similar Questions
A paraticale of mass m and charge (−q) enters the region between the two charged plates initially moving along x-axis with speed vx. The length of plate is L and a uniform electric field E is maintained between the plates. Show that the verticale deflection of the particle at the far edge of the plate is qEL2/(2mv2x). Compare this motion with motion of a projectille in gravitional field.
View SolutionA particle of mass m and charge -q enters the region between the two charged plates initially moving along x-axis with speed vx as shown in figure. The length of plate is L and a uniform electric field E is maintained between the plates. The vertical deflection of the particle at the far edge of the plate is
View Solution
Knowledge Check
A parallel plate condenser has a unifrom electric field E(V/m) in the space between the plates. If the distance between the plates is d(m) and area of each plate is A(m2) the energy (joule) stored in the condenser is
A12ε0E2Bε0EAdC12ε0E2AdDE2Ad∣ε0A uniform electric field →E exists between the plates of a charged condenser. A charged particle enters the space between the plates and perpendiculars to →E. The path of the particle between the plates is a
AStraight lineBhyperbolaCparabolaDcircleA positive charged particle P enters the region between two parallel plates with a velocit u, in a direction parallel to the plates. There is a uniform electric field in the region. P emerges from this region with a velocit v. Taking C as a constant v will depend on u as
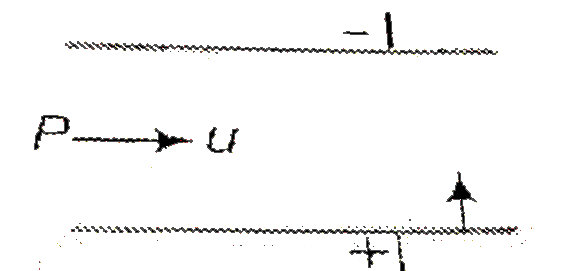 Av=CuBv=√u2+CuCv=√u2+CuDv=√u2+Cu2
Av=CuBv=√u2+CuCv=√u2+CuDv=√u2+Cu2
A particle of mass m and charge(-q) enters the region between the two charged plates intially moving along x - axis with speed Vx . The length of plate is L and a uniform electric field E is maintained between the plates . Show that the verticles deflection of the particle at the far edge of the palte is qEL2/(2mv2x).
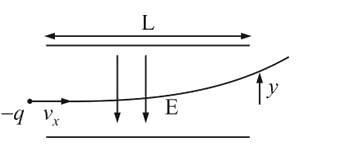
View SolutionA particle of mass m and charge (-q) enters the regions between the two charged plates initially moving along x-axis with speed vx (like particle 1 in.) The length of plate is L and an the particle at the far edge of the plate is qEL2/(2mv2x).
View SolutionFigure shows an assembly of deflecting plates A and B ofan ink-jet printer which causes moving ink droplets to deflect at desired displacements by continuously varying electric field between the plates. An ink drop with a mass m=1.3×10−10kg and a negative charge of magnitude q=1.5xx10−13C enters the region between the plates, initially moving along the x-axis with speed vx,=10m/s. The length of plates is L=1.6cm. The plates are connected with a varying voltage and thus produce an electric field at all points between them. Assume that field →E for some duration is constant and it is acting in downward direction as shown and has a magnitude of E=I.4×106N/C, find the vertical deflection of the drop at the far edge ofthe plate? As the gravitational force on the drop is very small relative to the electrostatic force acting on the drop, it can be neglected for this analysis. [6.4×10−4m]

View SolutionA parallel plate condenser has a unifrom electric field E(V/m) in the space between the plates. If the distance between the plates is d(m) and area of each plate is A(m2) the energy (joule) stored in the condenser is
View SolutionA parallel plate condenser has a unifrom electric field E(V/m) in the space between the plates. If the distance between the plates is d(m) and area of each plate is A(m2) the energy (joule) stored in the condenser is
View Solution
