Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss's law. [Hint.use Coulomb's law directly and evaluate the necessary integral ].
Take a long thin wire XY (as shown in the figure) of uniform linear charge density

Consider a point A at a perpendicular distance l from the mid-point O of the wire, as shown in the following figure.
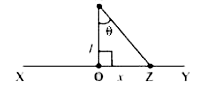
Let E be the electric field at point A due to the wire, XY.
Consider a small length element dx on the wire section with OZ = x
Let q be the charge on this piece.
∴=λdx
Electric field due to the piece,
dE=14πε0λdx(AZ)2
However,dZ=√(l3+x3)
∴dE=λdx4πε0(l2+x2)
The electric field is resolved into two rectangular components. dEcosθ is the perpendicular component and
∴dE1=λdxcosθ4π∈0(x2+l2) ...(1)
InΔAZO,
tanθ=xl
x=ltanθ ...(2)
On differrentiating equation (2), we obtain
dxdθ=lsec2θdx=lsec2θdθ
From equation (2),
x2+l2=l2+l2tan2θ
∴l2(1+tan2θ)=l2sec2θ
x2+l2=l2sin2θ ...(4)
Putting equations (3) and (4) in equation (1), we obtain
∴dE1=λlsec2dθ4π∈0l2sec2θ×cosθ
∴dE1=λcosθdθ4π∈0l ...(5)
The wire is so long that θ tends from −π2 to +π2
By intergrating equation (5), we obtain the value of field E1 as,
π2∫−π2dE1=π2∫−π2λ4π∈0lcosθdθ
E1=λ4π∈0l[sinθ]π2−π2
=λ4π∈0l×2
E1=λ2π∈0l
Therefore, the electric field due to long wire is λ2π∈0l.
Similar Questions
Knowledge Check
- Question 1 - Select One
The electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
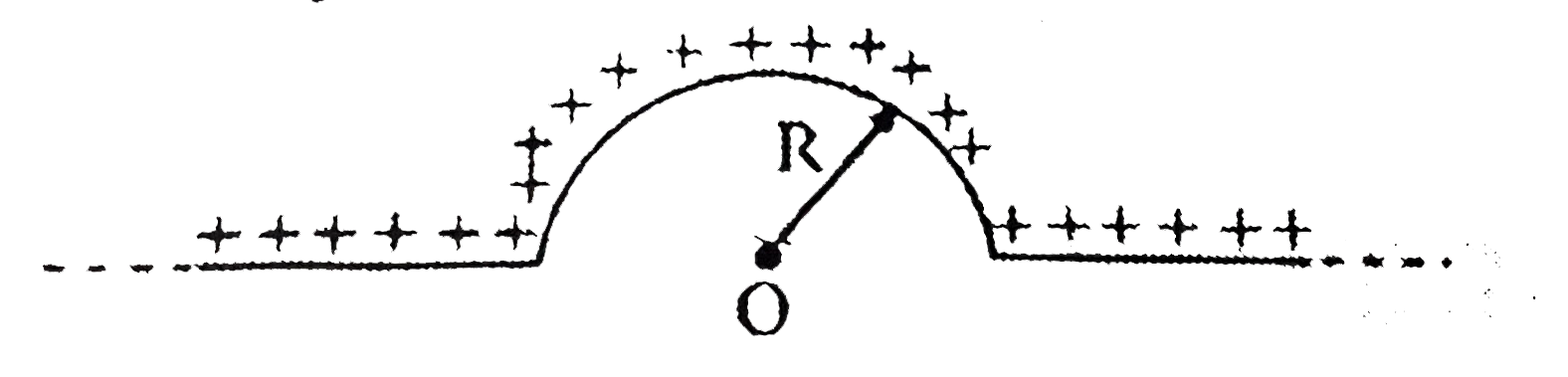 Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero - Question 2 - Select One
Twelve infinite long wire of uniform linear charge density (λ) are passing along the twelve edges of a cube. Find electric flux through any face of cube. ,
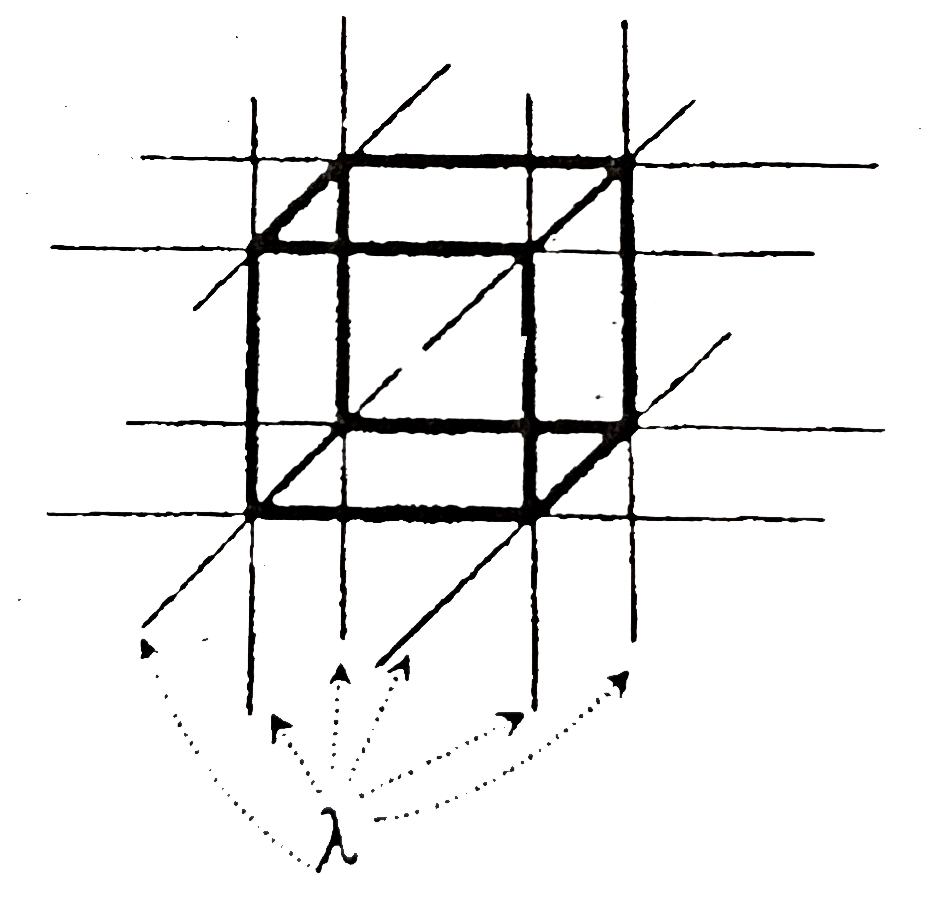 A(λl2ε0)B(λlε0)C(λl3ε0)D(3λlε0)
A(λl2ε0)B(λlε0)C(λl3ε0)D(3λlε0) - Question 3 - Select One
The electric field strength due to a circular loop of charge of radius R are uniform linear density of charge λ, at its centre is proportonal to
AλRBλ/RCλ/R2DNone of these
Write the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View SolutionState Gauss' law.Using this law obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ
(ii) A wire AB of length L has linear charge λ=kx, where x is measured from the end A of the wire. The wire is enclosed by a Gaussian hollow surface.Find the expression for the electric flux through the surface.View SolutionCalculation OF electric field using gauss law
View Solution(a) State Gauss's law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge desntiy λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.View SolutionIn the given arrangement find the electric field at C in the figure. Here the U-shaped wire is uniformly charged with linear charge density λ. [0]
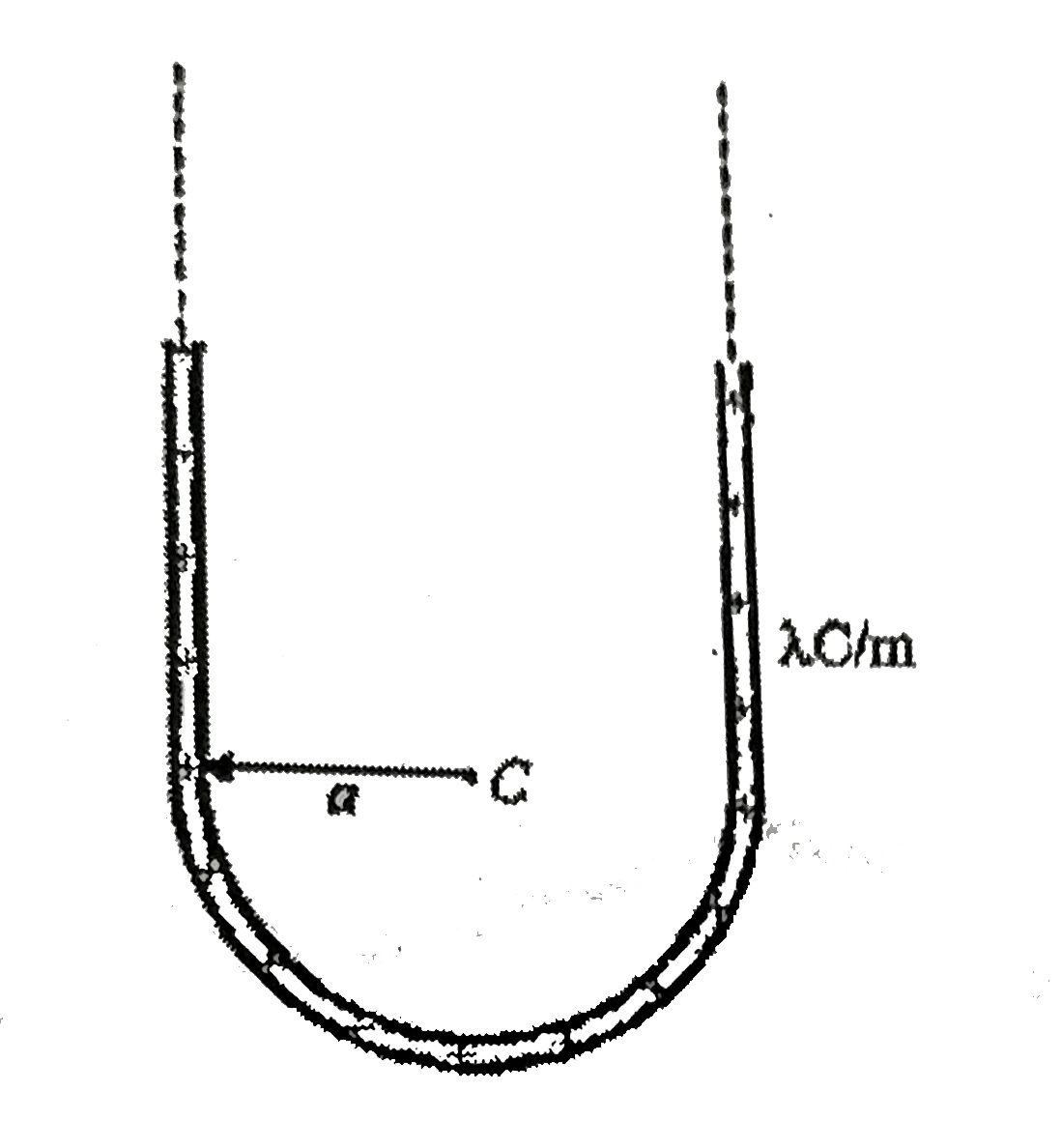 View Solution
View Solution


