A particle of mass m and charge q is moving in a region where uniform electric field −−→E and and uniform mag-netic field −−→Bare present. It is given that −−→E∣∣→E∣∣=−−→B∣∣→B∣∣. At time t = 0, velocity of the particle is −−→V0 and −−→V0.−−→E=0. Write the velocity of the particle at time t.
The correct Answer is:→Vcos(qBtm)→V0+(qtm)(→E)+sin(qBtm)(→V0×→BB)
Step by step video, text & image solution for A particle of mass m and charge q is moving in a region where uniform electric field underset(E)to and and uniform mag-netic field underset(B)toare present. It is given that underset(E)to/|vec(E)|=underset(B)to/|vec(B)|. At time t = 0, velocity of the particle is underset(V)to_(0) and underset(V)to_(0).underset(E)to=0. Write the velocity of the particle at time t. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-34videos
MOTION OF CHARGE IN MAGNETIC FIELD
- BOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-34videos
MOTION OF CHARGE IN MAGNETIC FIELD
- BOOK - ARIHANTCHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - Magnetic effect of Current45videos
MAGNETIC EFFECT OF CURRENT
- BOOK - ARIHANTCHAPTER - NUCLEAR PHYSICSEXERCISE - All Questions54videos
NUCLEAR PHYSICS
Similar Questions
A particle of mass m and charge q is moving in a region where uniform, constant electric and mangetic fields →Eand→B are present. →Eand→B are parallel to each other. At time t=0, the velocity →v0 of the particle is perpendicular to →E (Assume that its speed is always <<c, the speed of light in vacuum). Find the velocity →v of the particle at time t. You must express your answer in terms of t,q,m, the vector →v0,→E and →B and their magnitudes →v0,→E and →B.
View SolutionTwo identical charged particles are projected simul- taneously from origin in xy plane. Each particle has charge q and mass m and has been projected with velocity v as shown in the figure. There exists a uniform magnetic field B in negative z direction.
(i) Find −−→V1.−−→V2at time t where −−→V1and−−→V2 are velocities of the particles at time t.
Find −−→V1.−−→V2 at time t=πmqB where −−→r1.−−→V2are the position vectors of the two particles.
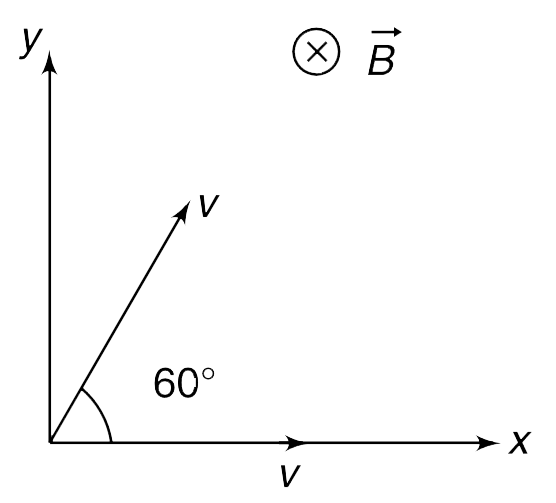 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
Astraight lineBellipseCparabolaDcircle - Question 2 - Select One
A particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
AAways circularBcircular, If v×B=0Ccircular,If v.B=0DNone of these - Question 3 - Select One
A particle ( mass = m and charge = q ) is moving in a region in which there exists a uniform electric field E→i and a uniform magnetic field Bˆk. At t = 0 , the particle is at ( 0,a ) and is moving with vˆi. After some time, the particle is located at ( 2a, 0 ) and has a velocity −2vˆj , then which of the following is true ?
AE=32(mv2qa)Bat the initial moment, the rate of work done by electric field is 34(mv3a)CE=38(mv2qa)Dat the initial moment, the rate of work done by electric field is 316(mv3a)
A particle of mass m and charge q is projected into a uniform magnetic field −−→B=−B0ˆK with velocity −−→V−V0ˆi from origin. The position vector of the particle at time t is −−→r. Find the impulse of magnetic force on the particle by the time −−→r.−−→V becomes zero for the first time.
View SolutionA charge particle enters into a region containing uniform electric field (E) and uniform magnetic field (B) along x-axis and y-axis respectively.If it passes the region undeviated the velocity of charge particle is given by
View SolutionA charge particle enters into a region containing uniform electric field (E) and uniform magnetic field (B) along x- axis and y-axis respectively.If it passes the region undeviated the velocity of charge particle is given by
View SolutionForce →F acting on a test charge q0 in a uniform electric field →E is
View SolutionForce →F acting on a test charge q0 in a uniform electric field →E is
View Solution

