A particle of mass (m) is attached to a spring (of spring constant k) and has a narural angular frequency omega_(0). An external force R(t) proportional to cos omegat(omega!=omega)(0) is applied to the oscillator. The time displacement of the oscillator will be proprtional to.
mω20−ω2
1m(ω20−ω2)
1m(ω21+ω2)
mω21+ω2
The correct Answer is:B
For forced oscillation,
x=x0sin(ωt+ϕ) and F=F0cosωt
where x0=F0m(ω20−ω2)∝1m(ω20−ω2)
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - AIIMS Questions24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk - Question 2 - Select One
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk - Question 3 - Select One
If a body of mass 0.98 kg is made to oscillate on a spring of force constant 4.84 N/m the angular frequency of the body is
A1.22 rad/sB2.22 rad/sC3.22 rad/sD4.22 rad/s
When a particle of mass m is attached to a vertical spring of spring constant k and released, its motion is described by y(t)=y0sin2ωt, where 'y' is measured from the lower end of unstretched spring. Then ω is :
View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
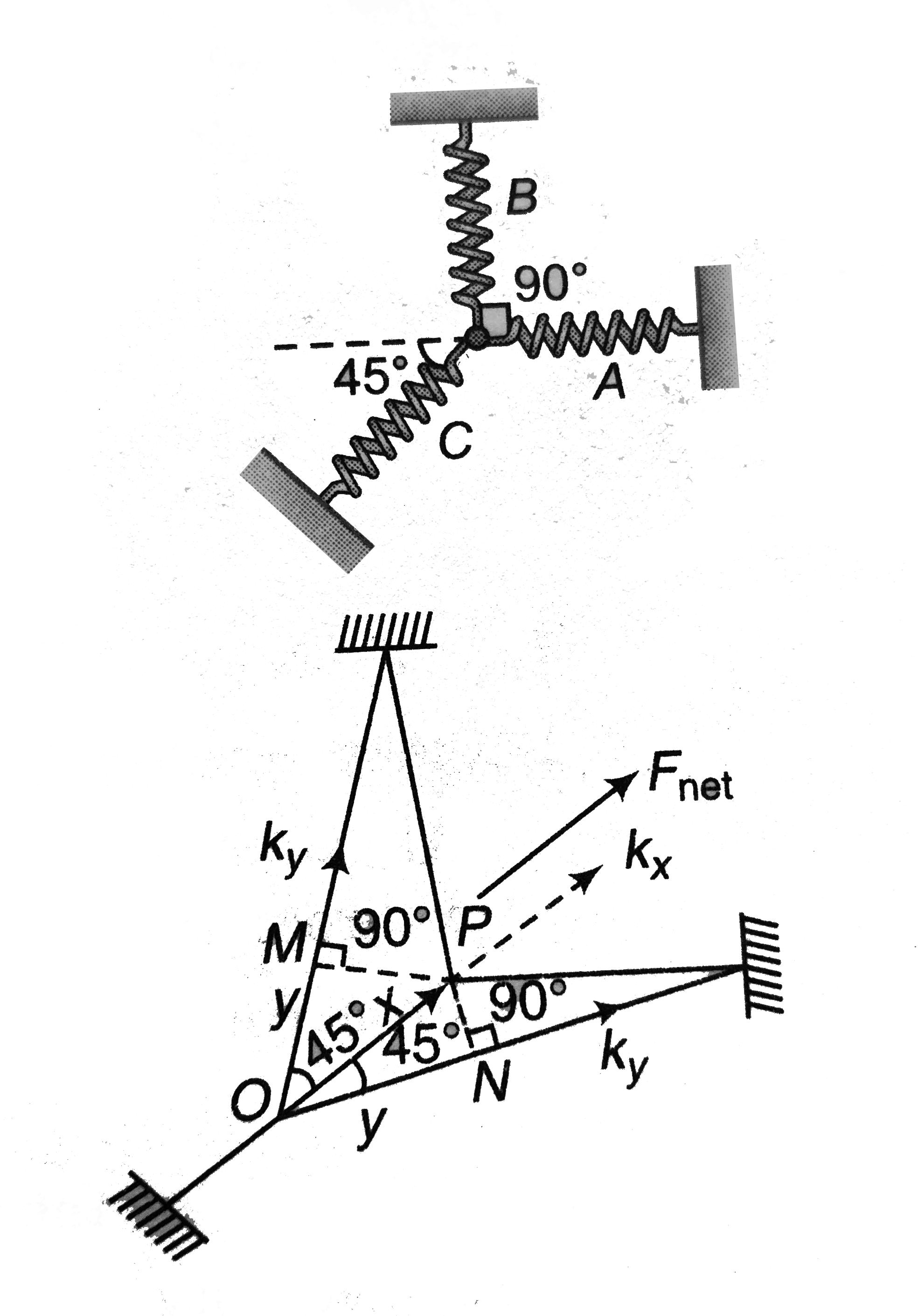 . View Solution
. View SolutionAn object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionA small mass m attached to one end of a spring with a negligible mass and an unstretched length L, executes vertical oscillations with angular frequency ω0 When the mass is rotated with an angular speed ω by holding the other end of the spring at a fixed point, the mass moves uniformly in a circular path in a horizontal plane. Then the increase in length of the spring during this rotation is
View Solution

