A particle of mass m is attached to a string of length L and given velocity √10gL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (i) lowest position (ii) highest position,
To solve the problem, we need to find the tension in the string when the particle is at two positions: the lowest point and the highest point.
Given:
- Mass of the particle = m
- Length of the string = L
- Initial velocity at the lowest point = v=√10gL
Step 1: Tension at the Lowest Position
1. Identify Forces at the Lowest Position:
At the lowest position, the forces acting on the particle are:
- Tension T1 acting upwards.
- Weight mg acting downwards.
2. Apply Newton's Second Law:
The net force acting on the particle is given by:
T1−mg=m⋅a
where a is the centripetal acceleration. Since the radius of the circular motion is L, we have:
a=v2L
3. Substituting for a:
T1−mg=m⋅v2L
4. Substituting the value of v:
Given v=√10gL, we find v2:
v2=10gL
5. Plugging v2 into the equation:
T1−mg=m⋅10gLL
Simplifying gives:
T1−mg=10mg
6. Solving for T1:
T1=10mg+mg=11mg
Step 2: Tension at the Highest Position
1. Identify Forces at the Highest Position:
At the highest position, the forces acting on the particle are:
- Tension T2 acting downwards.
- Weight mg also acting downwards.
2. Apply Newton's Second Law:
The net force acting on the particle is given by:
T2+mg=m⋅a
where a is again the centripetal acceleration:
a=v2L
3. Substituting for a:
T2+mg=m⋅v2L
4. Finding v2 at the highest position:
Using conservation of energy, the initial kinetic energy at the lowest point will equal the potential energy at the highest point plus the kinetic energy at the highest point:
12mv2=mg(2L)+12mv′2
where v′ is the velocity at the highest point.
5. Substituting v2:
12m(10gL)=mg(2L)+12mv′2
Simplifying gives:
5gL=2gL+12v′2
3gL=12v′2⟹v′2=6gL
6. Plugging v′2 into the equation for T2:
T2+mg=m⋅6gLL
Simplifying gives:
T2+mg=6mg
7. Solving for T2:
T2=6mg−mg=5mg
Final Answers:
- Tension at the lowest position T1=11mg
- Tension at the highest position T2=5mg
- Mass of the particle = m
- Length of the string = L
- Initial velocity at the lowest point = v=√10gL
At the lowest position, the forces acting on the particle are:
- Tension T1 acting upwards.
- Weight mg acting downwards.
The net force acting on the particle is given by:
T1−mg=m⋅a
where a is the centripetal acceleration. Since the radius of the circular motion is L, we have:
a=v2L
T1−mg=m⋅v2L
Given v=√10gL, we find v2:
v2=10gL
T1−mg=m⋅10gLL
Simplifying gives:
T1−mg=10mg
T1=10mg+mg=11mg
At the highest position, the forces acting on the particle are:
- Tension T2 acting downwards.
- Weight mg also acting downwards.
The net force acting on the particle is given by:
T2+mg=m⋅a
where a is again the centripetal acceleration:
a=v2L
T2+mg=m⋅v2L
Using conservation of energy, the initial kinetic energy at the lowest point will equal the potential energy at the highest point plus the kinetic energy at the highest point:
12mv2=mg(2L)+12mv′2
where v′ is the velocity at the highest point.
12m(10gL)=mg(2L)+12mv′2
Simplifying gives:
5gL=2gL+12v′2
3gL=12v′2⟹v′2=6gL
T2+mg=m⋅6gLL
Simplifying gives:
T2+mg=6mg
T2=6mg−mg=5mg
- Tension at the lowest position T1=11mg
- Tension at the highest position T2=5mg
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Solved Examples2videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Miscellaneous Examples5videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string is T and acceleration of the particle is a at any position then T. a' is positive at the lowest point for
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u . The tension in the string T and acceleration of the particle is a at any position. Then T.a is zero at highest point if
View SolutionA particle of mass m attached with a massless spring natural length l and stiffness k is released from rest from the horizontal position of the relaxed spring. When the particle passes through its lowest point, the maximum length of the spring becomes 2l. Find the:
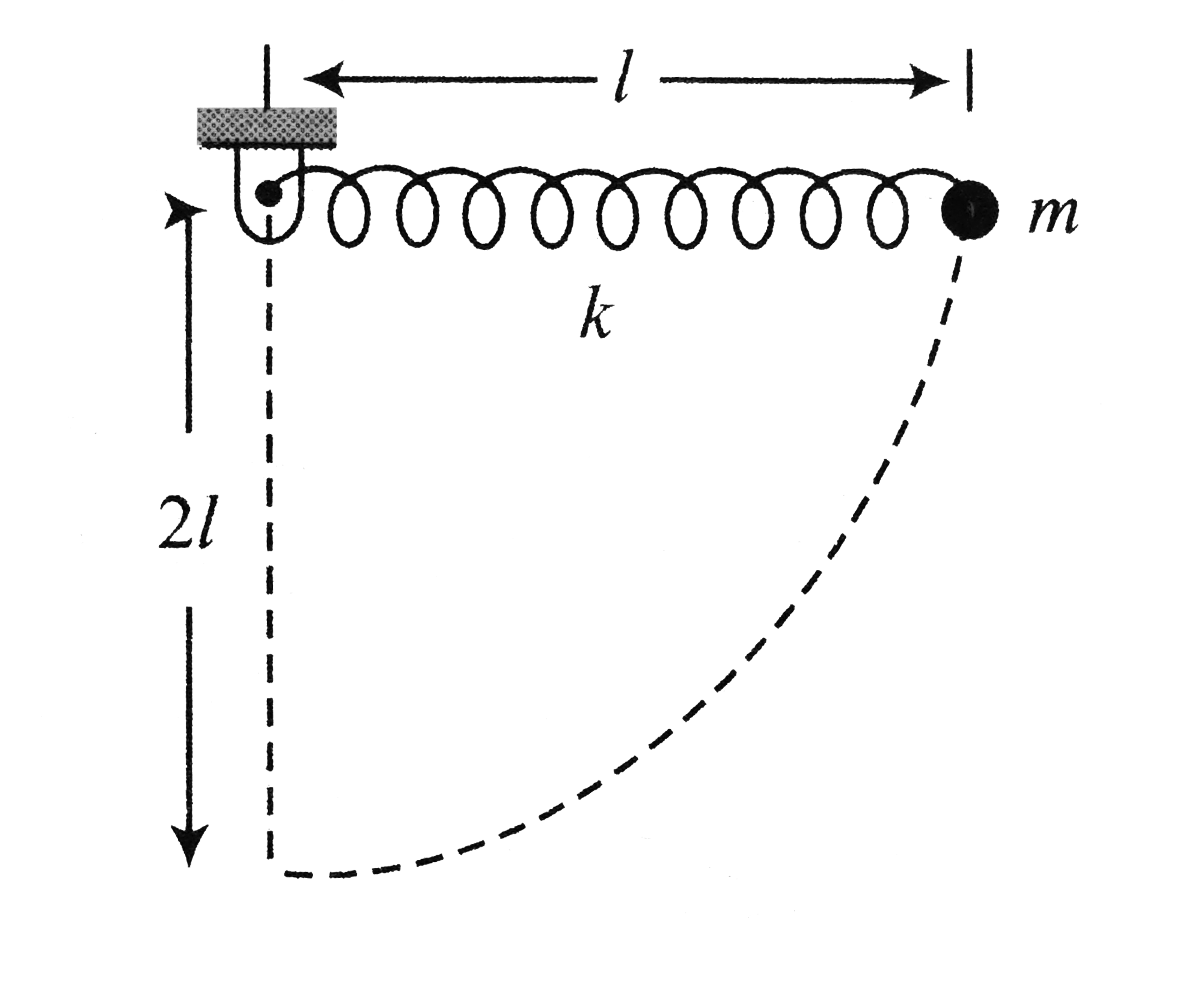
a. speed of the particle at its lowest point.
b. acceleration of the particle at its lowest position.View SolutionA stone of mass 0.5 kg is attached to a string of length 2 m and is whirled in a horizontal circle. If the string can with stand a tension of 9N, the maximum velocity with which the stone can be whirled is:
View SolutionA particle of mass m attached to a string of length l is descending circular motion on a smooth plane inclined at an angle α with the horizontal. For the particle to reach the highest point its velocity at the lowest point should exceed.
View SolutionA partical of mass m attached with a massless spring of natural length l and stiffness constant k is releaased from rest from the horizontal positon of the relaxed spring.

When the particle passes through its lowest point, the maximum length of the spring bocomes 2l find the
(A) Speed of the particle at its lowest point
(B) Acceleration of the particle at its lowest position.View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
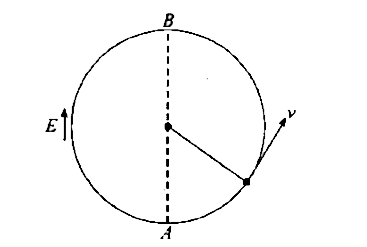 View Solution
View Solution

