A particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u . The tension in the string T and acceleration of the particle is a at any position. Then T.a is zero at highest point if
u>√5gl
u=√5gl
Both (a) and (b) are correct
Both (a) and (b) are wrong
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of the particle in a vertical circular path and apply the principles of dynamics and energy conservation.
Step 1: Understand the Forces Acting on the Particle
At the highest point of the circular path, the forces acting on the particle are:
- The gravitational force (mg) acting downward.
- The tension in the string (T) also acting downward.
At the highest point, the centripetal force required to keep the particle moving in a circle is provided by the combination of the gravitational force and the tension in the string. Therefore, we can write the equation for centripetal force as:
T+mg=mv2l
where v is the velocity of the particle at the highest point and l is the length of the string (which is also the radius of the circular path).
Step 2: Apply Conservation of Energy
To find the velocity v at the highest point, we can use the conservation of mechanical energy. The total mechanical energy at the lowest point (point A) is equal to the total mechanical energy at the highest point (point B).
At the lowest point, the energy is purely kinetic:
EA=12mu2
At the highest point, the energy is the sum of kinetic and potential energy:
EB=12mv2+mg(2l)
where 2l is the height gained when moving from the lowest point to the highest point.
Setting the energies equal gives us:
12mu2=12mv2+mg(2l)
Step 3: Solve for v2
Rearranging the equation to solve for v2:
12mu2−mg(2l)=12mv2
Multiplying through by 2 to eliminate the fraction:
mu2−4mgl=mv2
Dividing by m:
u2−4gl=v2
Step 4: Set Tension to Zero
According to the problem, we need to find the condition when T.a=0 at the highest point. This implies that the tension T must be zero at the highest point:
0+mg=mv2l
Substituting T=0 into the centripetal force equation gives:
mg=mv2l
Canceling m from both sides:
g=v2l
Substituting v2=u2−4gl into this equation:
g=u2−4gll
Step 5: Solve for u
Rearranging gives:
gl=u2−4gl
Adding 4gl to both sides:
5gl=u2
Taking the square root:
u=√5gl
Conclusion
Thus, the initial velocity u at the lowest point must be √5gl for the tension in the string to be zero at the highest point.
At the highest point of the circular path, the forces acting on the particle are:
- The gravitational force (mg) acting downward.
- The tension in the string (T) also acting downward.
T+mg=mv2l
where v is the velocity of the particle at the highest point and l is the length of the string (which is also the radius of the circular path).
To find the velocity v at the highest point, we can use the conservation of mechanical energy. The total mechanical energy at the lowest point (point A) is equal to the total mechanical energy at the highest point (point B).
EA=12mu2
EB=12mv2+mg(2l)
where 2l is the height gained when moving from the lowest point to the highest point.
12mu2=12mv2+mg(2l)
Rearranging the equation to solve for v2:
12mu2−mg(2l)=12mv2
Multiplying through by 2 to eliminate the fraction:
mu2−4mgl=mv2
Dividing by m:
u2−4gl=v2
According to the problem, we need to find the condition when T.a=0 at the highest point. This implies that the tension T must be zero at the highest point:
0+mg=mv2l
Substituting T=0 into the centripetal force equation gives:
mg=mv2l
Canceling m from both sides:
g=v2l
Substituting v2=u2−4gl into this equation:
g=u2−4gll
Rearranging gives:
gl=u2−4gl
Adding 4gl to both sides:
5gl=u2
Taking the square root:
u=√5gl
Thus, the initial velocity u at the lowest point must be √5gl for the tension in the string to be zero at the highest point.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string is T and acceleration of the particle is a at any position then T. a' is positive at the lowest point for
View SolutionA particle of mass m is attached to a string of length L and given velocity √10gL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (i) lowest position (ii) highest position,
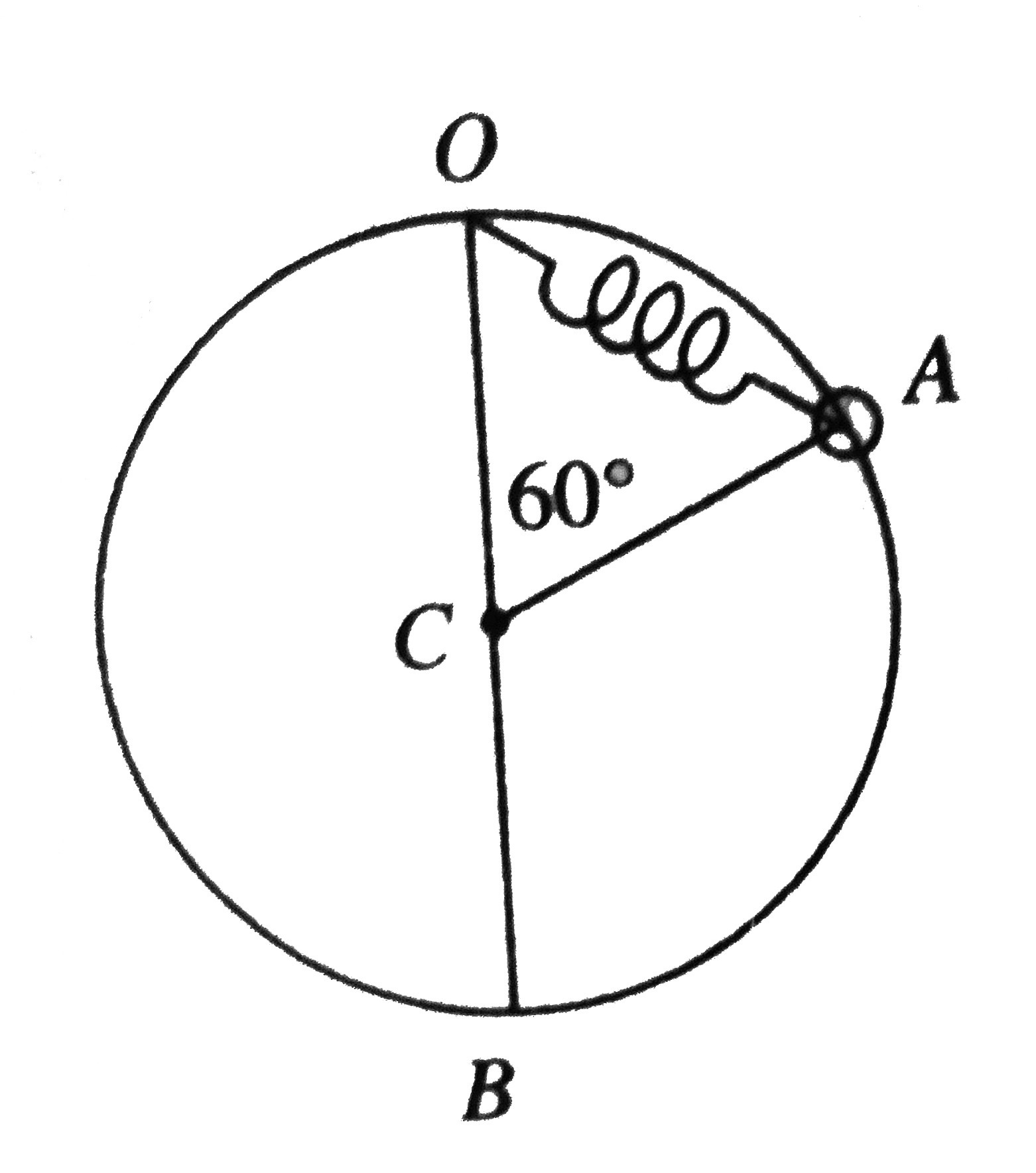
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View SolutionA particle tied to a string moves in a circular path in vertical plane. Its velocity at lowerst point is such that it just completes circle. Find the ratio of resultant force on particle at the lowerst point to that at highest point.
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA particle is fastened at the end of a string and whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View Solution
