A particle of mass m is attached to one end of a mass-less spring of force constant k, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time t=0 with an initial velocity u0. when the speed of the particle is 0.5u0, it collides elastically with a rigid wall. After this collision
the speed of the particle when it returns to its equilibrium position is u0.
the time at which the particle passes through the equilibrium position for the first time is t=π√mk
the time at which the maximum compression of the spring occurs is t=4π3√mk
the time at which the particle passes through the equilibrium position for the second time is t=5π3√mk.
The correct Answer is:A, D
v=u0sinωt
(suppose t01 is the time of collision)
u02=u0cosωt1⇒t1=π3ω
Now the particle returns to equilibrium position at time t2=2t1 i.e., 2π3ω with the same mechanical energy i.e., its speed will be u0. Let t be the time at which the particle passes through the equilibrium position for the second time.
Energy of particle and spring remains conserved.
t2=T2+2t1=πω+2π3ω=5π3ω=5π3√mk.
Topper's Solved these Questions
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICSCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Comprehension
12 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICSCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer
4 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICSCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Single Correct
51 Videos
- ARCHIVES 1 VOLUME 6BOOK - CENGAGE PHYSICSCHAPTER - ARCHIVES 1 VOLUME 6EXERCISE - Integer
4 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
Similar Questions

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View Solution
Knowledge Check
A small block of mass m is attached to free end of a spring of force cosntant k , whose other end is fixed to a rigid support . The block is lying on a frictionless horizontal plane and it starts movi0ng away from fixed end of the spring a\t t= 0 with intial velocity u When the speed of the block is 0.6μ it collides with a fixed heavy mass elastically. After the collision with a fixed heavy mass elastically . Aftere the collision the time at which the block passes through its equilibrium position for the first time is close to
Aπ√mKB1.86√mKC2√mKD2π√mKA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
Amω2l0kBmω2l0k−mω2Ckl0k−mω2Dmω2l0k+mω2A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
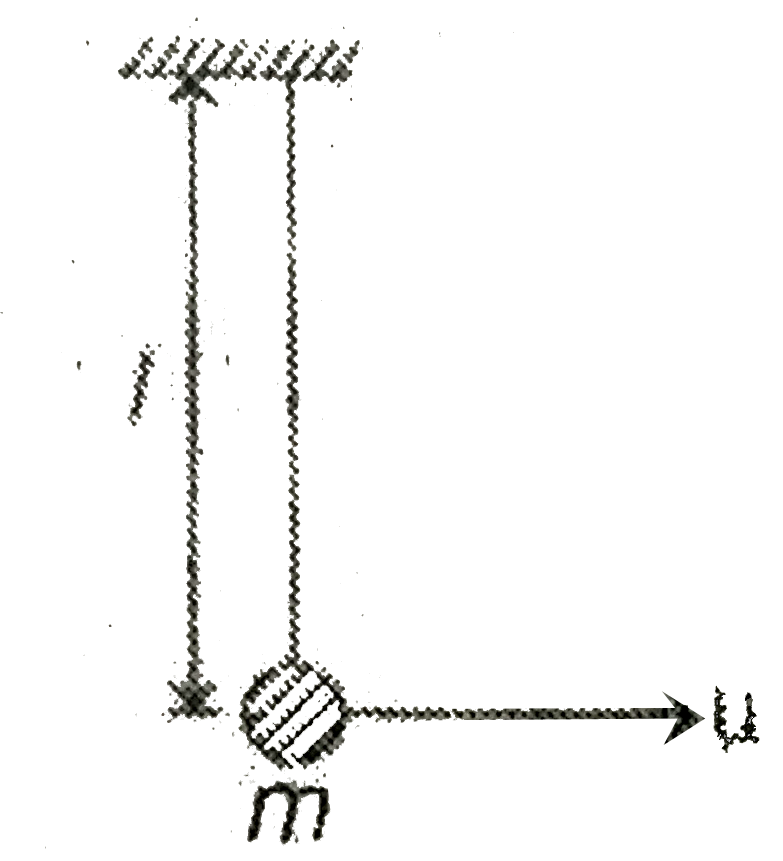
The maximum angle made by the string with downward vertical isAcos−1(14)Bsin−1(14)Cπ2+cos−1(14)Dπ−cos−1(14)
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

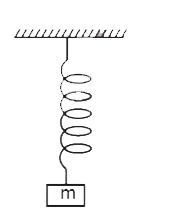
View SolutionA mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
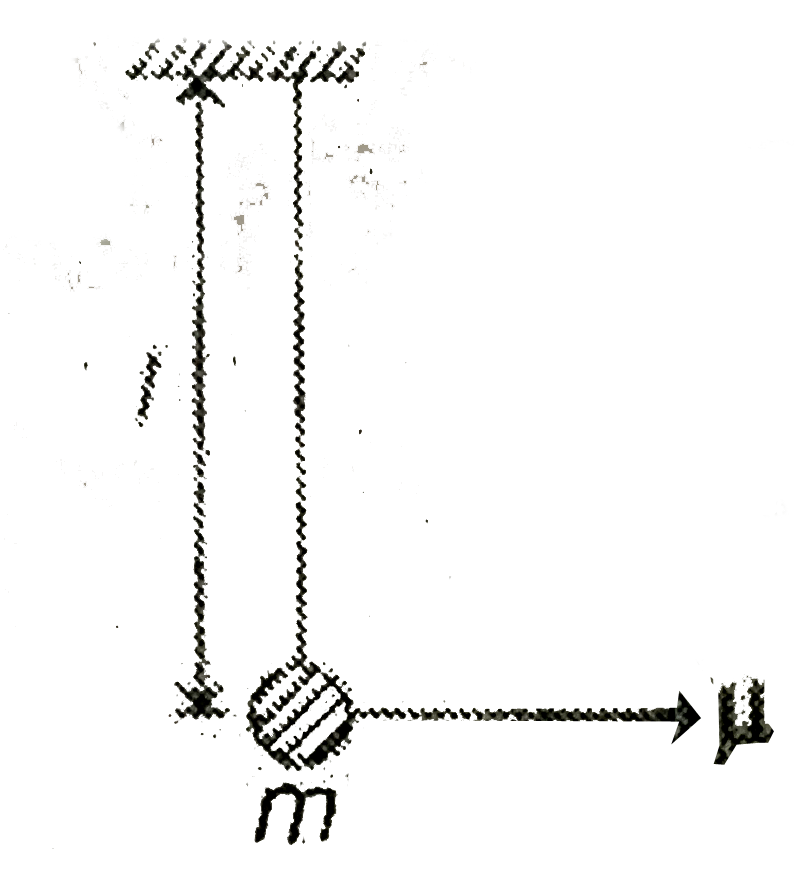
The tension in the string at an instant when acceleration of the particle is horizontal and √3g is
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution
