A particle of mass m is attached to one end of a weightless and inextensible string of length L. The particle is on a smooth horizontal table. The string passes through a hole in the table and to its other and is attached a small particle of equal mass m. The system is set in motion with the first particle describing a circle on the table with constant angular velocity ω1 and the second particle moving in the horizontal circle as a conical pendulum with constant angular velocity ω2 Show that the length of the portions of the string on either side of the hole are in the ratio ω22:ω21
Step by step video & image solution for A particle of mass m is attached to one end of a weightless and inextensible string of length L. The particle is on a smooth horizontal table. The string passes through a hole in the table and to its other and is attached a small particle of equal mass m. The system is set in motion with the first particle describing a circle on the table with constant angular velocity omega_(1) and the second particle moving in the horizontal circle as a conical pendulum with constant angular velocity omega_(2) Show that the length of the portions of the string on either side of the hole are in the ratio omega_(2)^(2): omega_(1)^(2) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Practice Exercise
42 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Discussion Question
31 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A particle of mass m is attacted to one end of string of length 3L. The particle is on a smooth horizontal table. The string passes through a hole in the table and to its other end is attached to a small particle of mass m0. The particle describe horizontal circular motion with angular velocity ω1 and ω2. find the value of (a) ω1ω2 and (b) the value of (1ω21+1ω22).
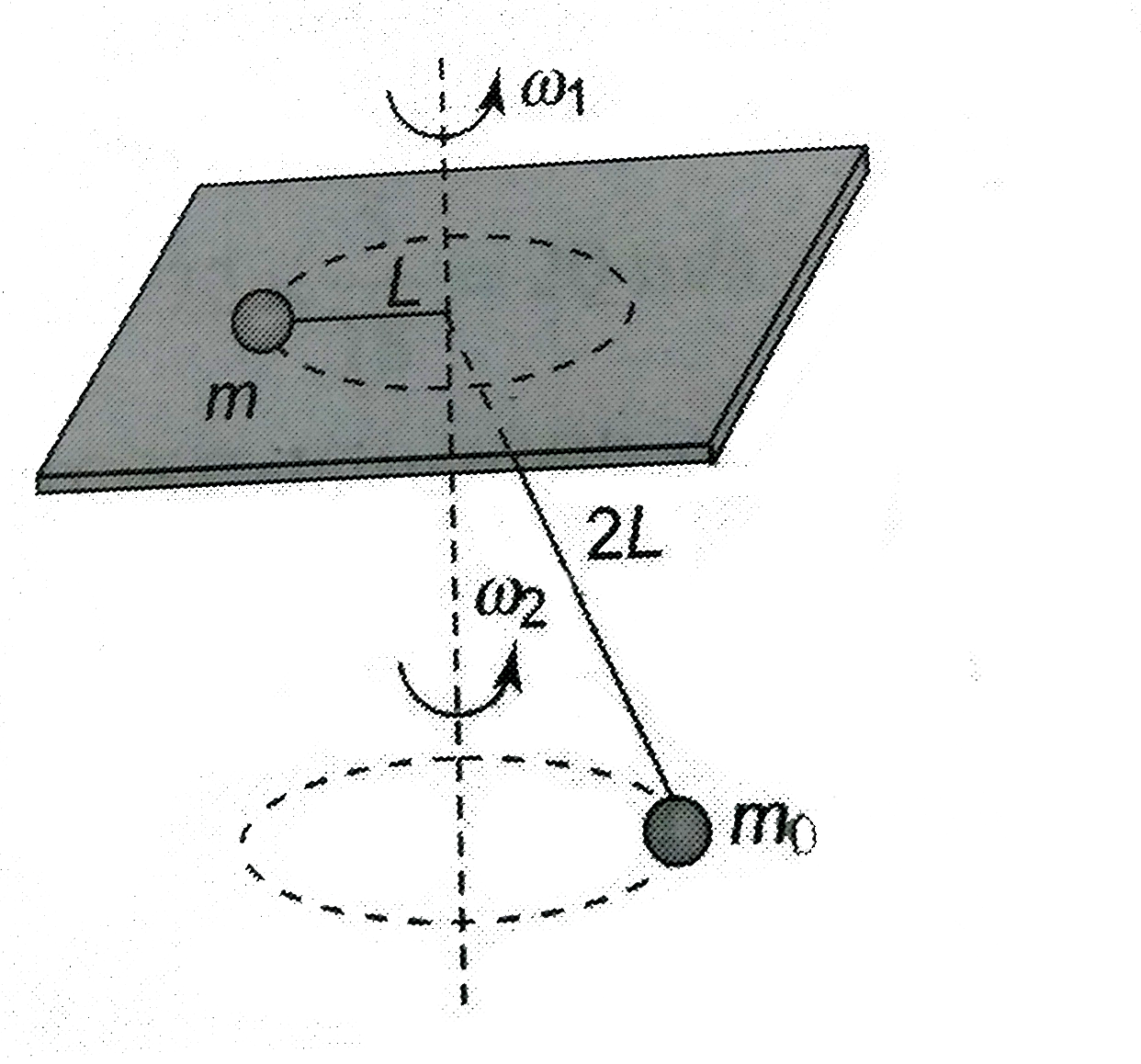
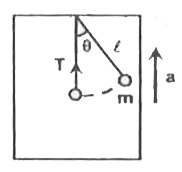
View SolutionA particle of mass m is attached to the celling of a cabin with an inextensible light string of length l. The cabin is moving upward with an acceleration a . The particle is taken to a position such that string makes an angle θ with vertical. When string becomes vertical, find the tension in the string.
View Solution
Knowledge Check
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12Two particles, each of mass m are attached to the two ends of a light string of length l which passes through a hole at the centre of a table. One particle describes a circle on the table with angular velocity ω1 and the other describes a circle as a conical pendulum with angular velocity ω2 below the table as shown in figure -3.86. if l1 and l2 are the lengths of the portion of the string above and below the table then :
 Al1l2=ω22ω21Bl1l2=ω21ω22C1ω21+1ω22=lgD1ω21+1ω22>lg
Al1l2=ω22ω21Bl1l2=ω21ω22C1ω21+1ω22=lgD1ω21+1ω22>lgA particle of mass m is attached to one end of a string of length l while the other end is fixed to a point h above the horizontal table. The particle is made to revolve in a circle on the table so as to make p revolutions per second. The maximum value of p if the particle is to be in contact with the table will be :
A2π√ghB√g/hC2π√h/gD12π√g/h
A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
View SolutionOne end of a string is attached to a 6kg mass on a smooth horizontal table. The string passes over the edge of the table and to its other end is attached a light smooth pulley.Over this pulley passes another string to the ends of which are attached masses of 4kg and 2kg respectively. Show that the 6kg mass moves with an acceleration of 8g/17.
View SolutionTwo identical particle are attached at the ends of a light string which passes through a hole at the centre of a table another particle on the table is made to revolve with angular velocity ω1 . One of the particles is made to move in a horizontal circle as a conical pendulum with angular velocity ω2 . If l1 and l2 are the length of the string over and under the table , then in order that particle under the table neither moves down nor moves up the ratio l1l2 is :

View SolutionA particle of mass m is attached to one end of string of length l while the other end is fixed to point h(h<l) above a horizontal table. The particle is made to revolve in a circle on the table so as to make p revolutions per second. The maximum value of p, if the particle is to be in contact with the table, is : (l>h)
View SolutionA bead of mass m is attached to the mid-point of a taut, weightless string of length l and placed on a frictionless horizontal table.
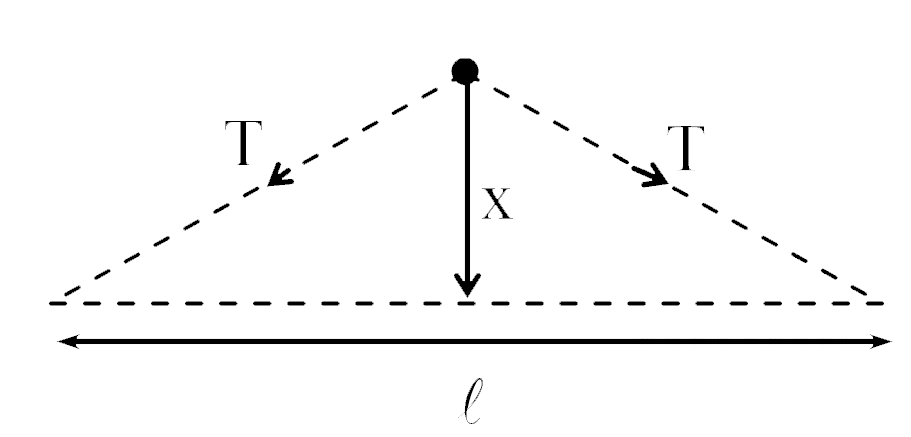
Under a small transverse displacement x, as shown, if the tension in the string is T, then the frequency of oscillation is-
View Solution
