A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
√rg
√2rg
2√rg
√rg2
To solve the problem, we will follow these steps:
Step 1: Understand the setup
A particle of mass m is suspended from a ceiling by a string of length L and moves in a horizontal circle of radius r. We are given that r=L√2.
Step 2: Identify the forces acting on the particle
The forces acting on the particle are:
- The gravitational force mg acting downwards.
- The tension T in the string, which can be resolved into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
Step 3: Set up the equations for vertical and horizontal forces
1. Vertical Force Balance:
The vertical component of the tension must balance the weight of the particle:
Tcosθ=mg(1)
2. Horizontal Force Balance:
The horizontal component of the tension provides the centripetal force required for circular motion:
Tsinθ=mv2r(2)
Step 4: Relate the angle θ to the geometry of the problem
Using the geometry of the situation, we can find tanθ:
- The vertical distance from the ceiling to the particle is x.
- The radius of the circle is r.
From the right triangle formed, we have:
tanθ=xr
Using the Pythagorean theorem:
x2+r2=L2
Substituting r=L√2:
x2+(L√2)2=L2
x2+L22=L2
x2=L2−L22=L22
Thus, x=L√2.
Now substituting back into tanθ:
tanθ=xr=L√2L√2=1
This implies:
θ=45∘
Step 5: Substitute tanθ into the equations
From equation (1):
Tcosθ=mg⟹T⋅1√2=mg⟹T=mg√2(3)
From equation (2):
Tsinθ=mv2r⟹T⋅1√2=mv2L√2
Substituting T from equation (3):
mg√2⋅1√2=mv2L√2
This simplifies to:
mg=mv2√2L
Cancelling m (assuming m≠0):
g=v2√2L
Rearranging gives:
v2=gL√2
Taking the square root:
v=√gL√2
Final Answer
The speed of the particle is:
v=√g⋅r
where r=L√2.
A particle of mass m is suspended from a ceiling by a string of length L and moves in a horizontal circle of radius r. We are given that r=L√2.
The forces acting on the particle are:
- The gravitational force mg acting downwards.
- The tension T in the string, which can be resolved into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
1. Vertical Force Balance:
The vertical component of the tension must balance the weight of the particle:
Tcosθ=mg(1)
The horizontal component of the tension provides the centripetal force required for circular motion:
Tsinθ=mv2r(2)
Using the geometry of the situation, we can find tanθ:
- The vertical distance from the ceiling to the particle is x.
- The radius of the circle is r.
tanθ=xr
Using the Pythagorean theorem:
x2+r2=L2
Substituting r=L√2:
x2+(L√2)2=L2
x2+L22=L2
x2=L2−L22=L22
Thus, x=L√2.
tanθ=xr=L√2L√2=1
This implies:
θ=45∘
From equation (1):
Tcosθ=mg⟹T⋅1√2=mg⟹T=mg√2(3)
Tsinθ=mv2r⟹T⋅1√2=mv2L√2
Substituting T from equation (3):
mg√2⋅1√2=mv2L√2
This simplifies to:
mg=mv2√2L
Cancelling m (assuming m≠0):
g=v2√2L
Rearranging gives:
v2=gL√2
Taking the square root:
v=√gL√2
The speed of the particle is:
v=√g⋅r
where r=L√2.
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B)
40 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
Consider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.

View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. Particle is imparted a horizontal velocity u=√2gl. Find the angle made by the string with the vertical when the acceleration of the particle is inclined to the string by 45∘?
View Solution
Knowledge Check
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12A particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
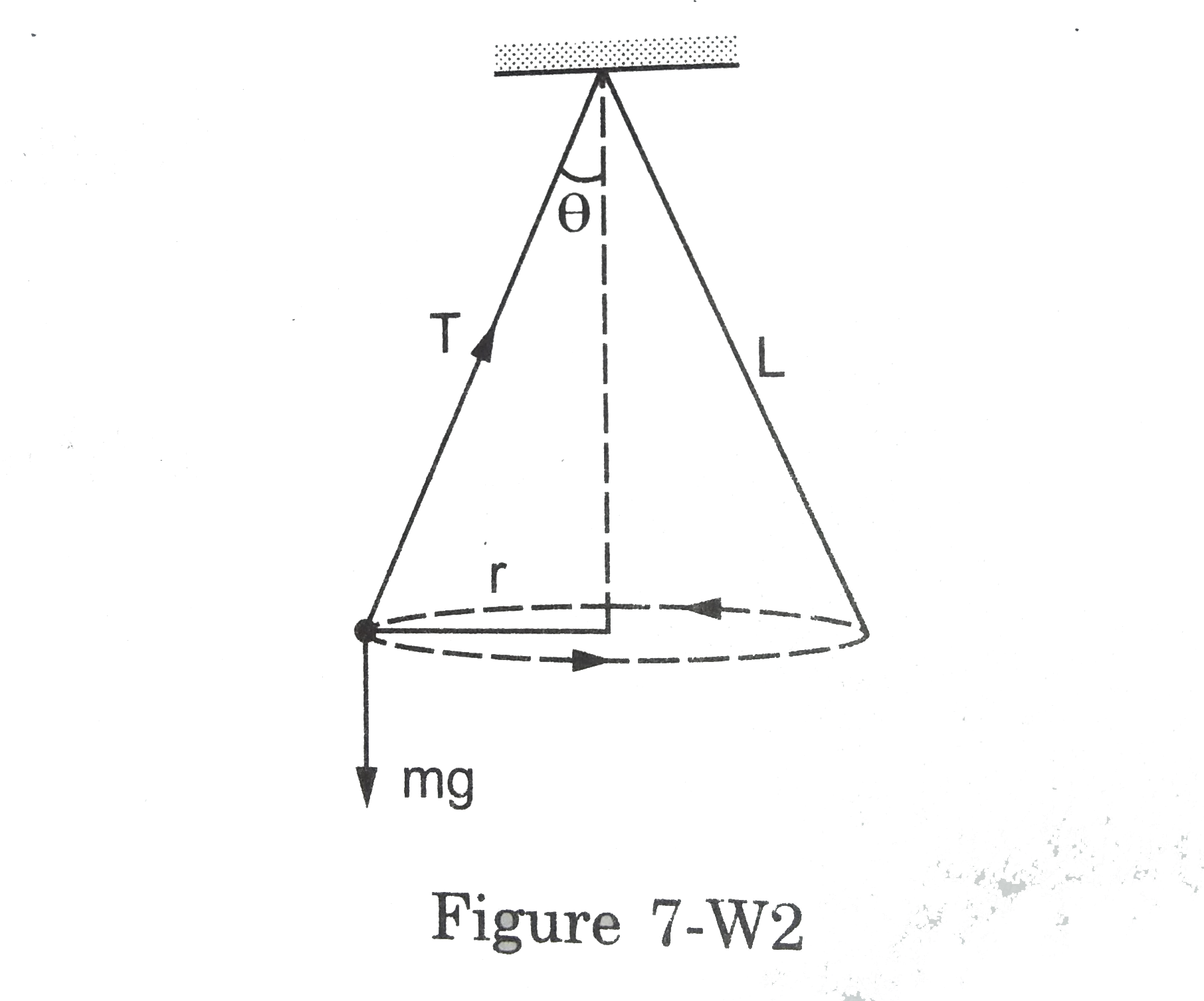
.Av=r√g(L2−r2)14andT=mgL(L2−r2)12Bv=r2√g(L3−r3)14andT=mgL(L2−r2)12Cv=r√g(L2−r2)14andT=mgL2(L2−r2)12Dv=r√g(L2−r2)14andT=mgL(L2−r2)14A paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are
 AmgandTBmg,T,mv2rdirected in wardsCmg,T,mv2rdirected outewardsDmv2ronly
AmgandTBmg,T,mv2rdirected in wardsCmg,T,mv2rdirected outewardsDmv2ronly
A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.

View SolutionA particle of mass m suspended by a string of length l revolves in a horizontal circle such that θ is the angle which the string makes with vertical. Which of the following statement (s) is/are correct ?
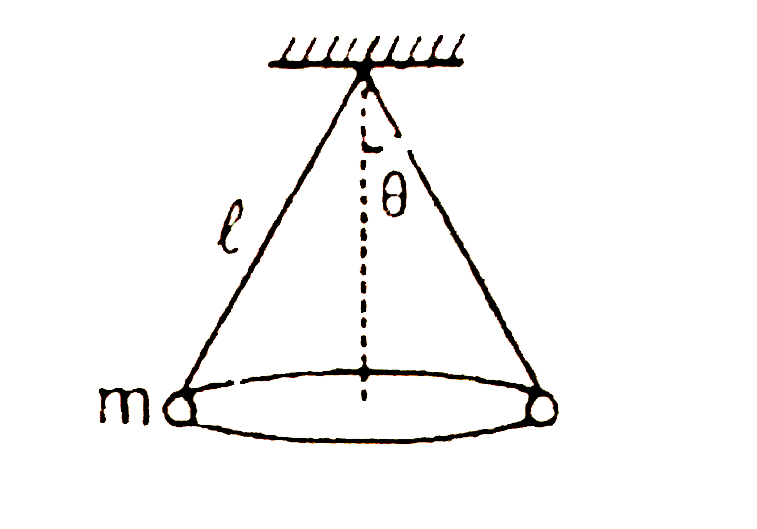
View SolutionIf KE of the particle of mass m performing UCM in a circle of radius r is E. Find the acceleration of the particle
View SolutionA particle of mass m suspended by a string of length l revolves in a horizontal circle (θ is the angle the string makes with vertical). Which of the following statement(s) is // are correct?
View Solution