A particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
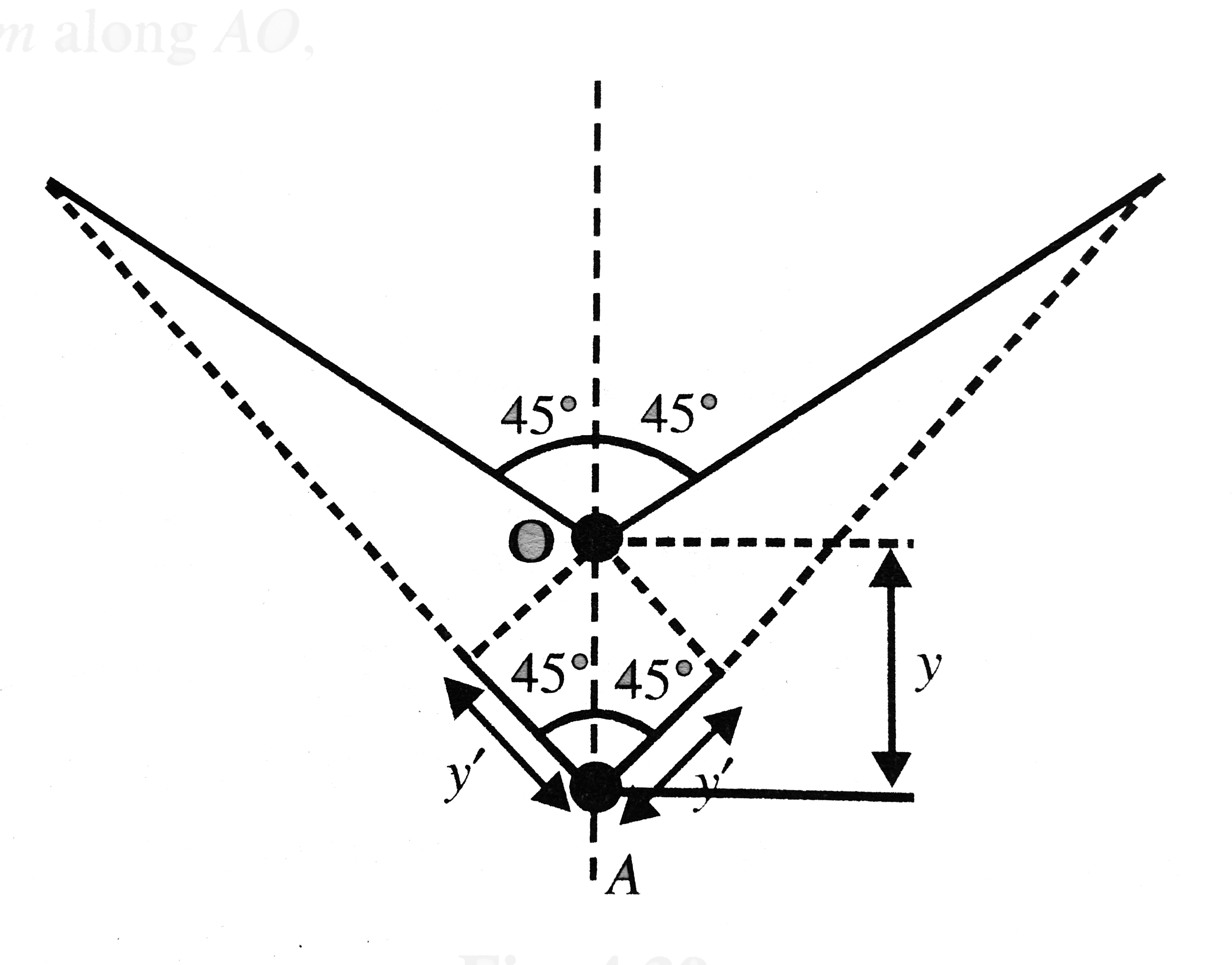
When the partical of mass m at O is pushed by y in the direction of A , spring A will be compressed by y while BandC will be stetched by y=ycos45∘ , so the total restoring force on mass m alongAo,
RF=FA+FBcos45∘+FCcos45∘
=ky+2(ky')cos45∘
Ky+2k(ycos45∘)cos45∘
F=(2k)y⇒ma=−(2k)y
Hence a==(2km)y as compared with a=−ω2y
We get ω2=2km which gives T=2π√m2k
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
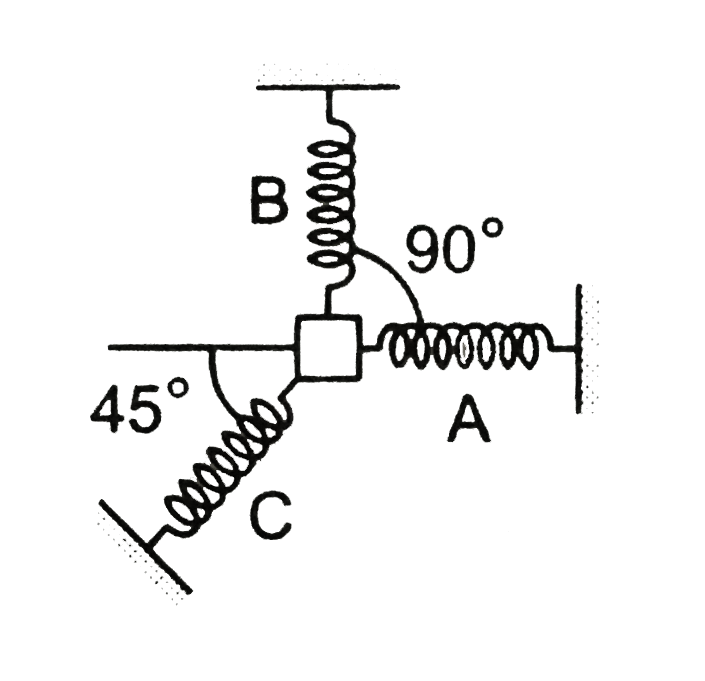
A particle of mass m is asttached to three springs A,B and C of equla force constants k as shown in figure. If the particle is pushed slightly against the spring C and released, find the time period of oscillastion.
View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
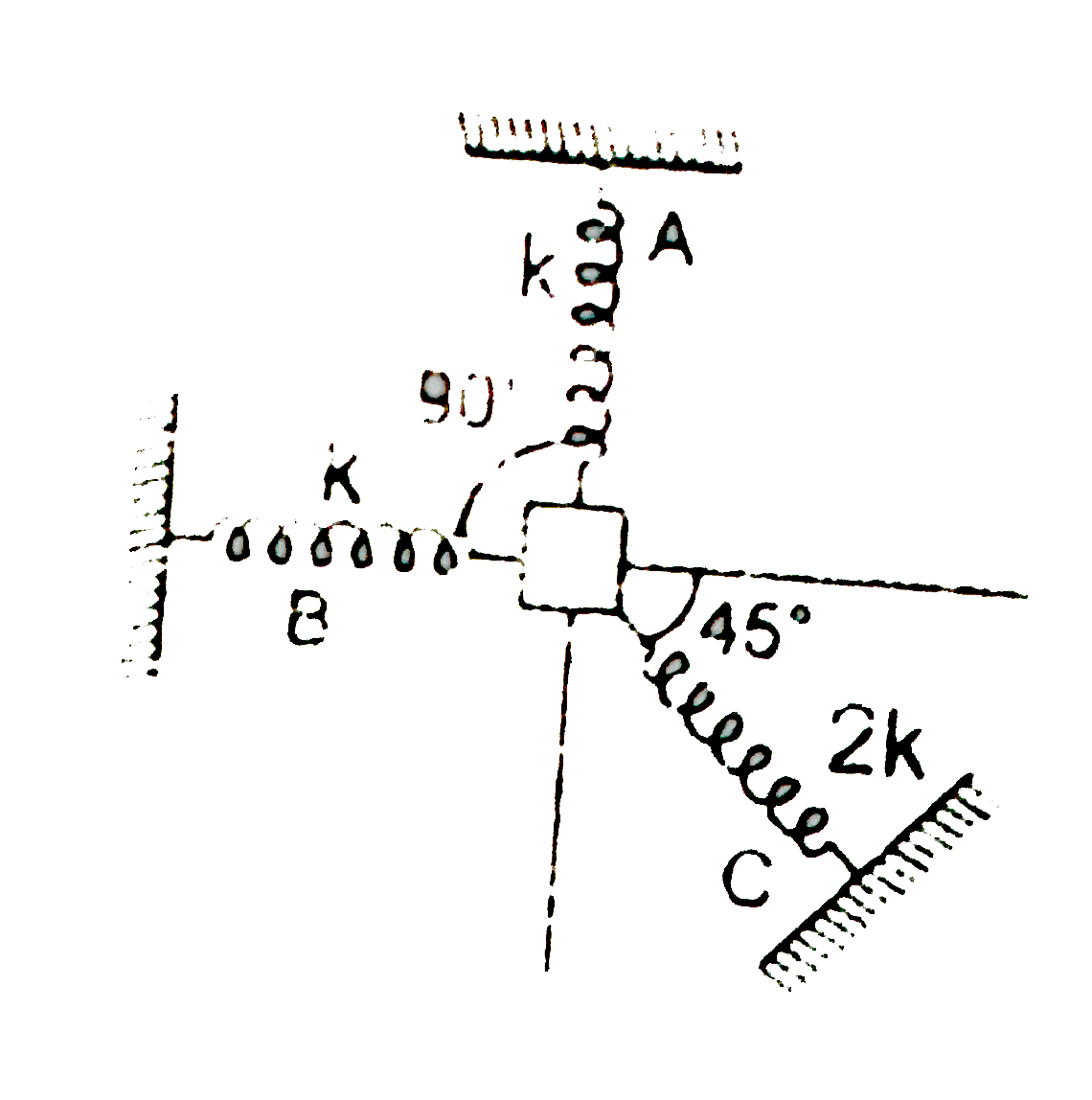
View Solution
Knowledge Check
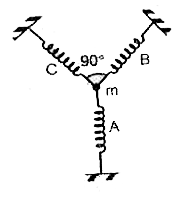
A particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
 AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mKA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkThree springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
The end of the rod which is connected to the spring is pushed down and released. Find time period of oscillation of the rod ?
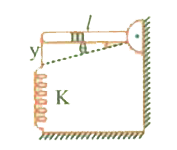
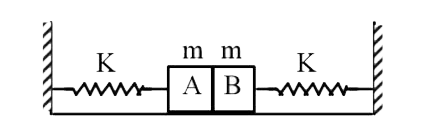
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
View SolutionA small block is connected to a mass less rod, which is turn is attached to a spring of force constant k as shown in Fig. The blcok is displaced down slightly, and left free. Find time period of small oscillations.
View SolutionA solid sphere of mass M and Radius R is attached to a massless spring of force constant k as shown in the figure. The cylinder is pulled towards right slightly and released so that it executes simple harmonic motion of time period. If the cylinder rolls on the horizontal surface without slipping, calculate its time period of oscillation.

View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View Solution
