A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

2π√mk
2π√m2k
2π√m3k
π√mk
The correct Answer is:B
When the particle of mass m at O is pushed by y in the direction of A, spring A will be compressed by y while springs B and C will be stretched by y.=ycos45∘
The total restoring force on the mass m along AO, is
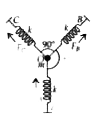
F=FA+FBcos45∘+FCcos45∘
F=−ky−ky.cos45∘−ky.cos45∘
F=−[ky+ky.cos45∘+ky.cos45∘]=−[ky+2ky.cos45∘]
=−[ky+2kycos245∘]=−[ky+ky]
F=−2ky........(i)
Comparing (i) with, F=−keqy, we get
keq=2k
The time period of vertical oscillations of the particle is,
T=2π√mkeq=2π√m2k
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - MTG-WBJEECHAPTER - OSCILLATIONS AND WAVESEXERCISE - WB JEE WORKOUT (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
10 Videos
- OSCILLATIONS AND WAVESBOOK - MTG-WBJEECHAPTER - OSCILLATIONS AND WAVESEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 1: SINGLE OPTION CORRECT TYPE (1 MARK))
16 Videos
- OSCILLATIONS AND WAVESBOOK - MTG-WBJEECHAPTER - OSCILLATIONS AND WAVESEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
2 Videos
- NUCLEAR PHYSICBOOK - MTG-WBJEECHAPTER - NUCLEAR PHYSICEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
5 Videos
- PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISMBOOK - MTG-WBJEECHAPTER - PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISMEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
15 Videos
Similar Questions
A block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is

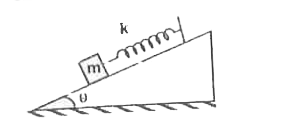
View SolutionA block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)
View Solution
Knowledge Check
A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
 AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mKA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
 A2π√mkB2π√2m3kCπ√3m2kDπ√2m3k
A2π√mkB2π√2m3kCπ√3m2kDπ√2m3k
A block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)

View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is

View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is

View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

View SolutionFive identical springs are used in the three configurations a shown in figure. The time periods of vertical oscillations in configurations (a), (b) and (c ) are in the ratio :
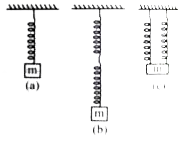
View Solution
