A particle of mass m is fixed to one end of a light rigid rod of length l and rotated in a vertical circular path about its other end. The minimum speed of the particle at its highest point must be
zero
√gl
√1.5gl
√2gl
The correct Answer is:A
To find the minimum speed of a particle of mass m at its highest point when it is attached to a rigid rod of length l and rotates in a vertical circular path, we can analyze the forces acting on the particle at that point.
1. Identify the Forces at the Highest Point:
At the highest point of the circular motion, the forces acting on the particle are:
- The gravitational force acting downward, which is mg (where g is the acceleration due to gravity).
- The tension in the rod (which we will denote as T) acting downward as well.
2. Apply Newton's Second Law:
At the highest point, the centripetal force required to keep the particle moving in a circular path is provided by the sum of the gravitational force and the tension in the rod:
mv2l=mg+T
where v is the speed of the particle at the highest point.
3. Determine the Minimum Speed Condition:
The minimum speed occurs when the tension T in the rod is zero (i.e., the rod is just taut and not under any tension). Thus, we can set T=0:
mv2l=mg
4. Solve for the Minimum Speed v:
Rearranging the equation gives:
mv2=mgl
Dividing both sides by m (assuming m≠0):
v2=gl
Taking the square root of both sides, we find:
v=√gl
5. Conclusion:
Therefore, the minimum speed of the particle at its highest point must be:
v=√gl
At the highest point of the circular motion, the forces acting on the particle are:
- The gravitational force acting downward, which is mg (where g is the acceleration due to gravity).
- The tension in the rod (which we will denote as T) acting downward as well.
At the highest point, the centripetal force required to keep the particle moving in a circular path is provided by the sum of the gravitational force and the tension in the rod:
mv2l=mg+T
where v is the speed of the particle at the highest point.
The minimum speed occurs when the tension T in the rod is zero (i.e., the rod is just taut and not under any tension). Thus, we can set T=0:
mv2l=mg
Rearranging the equation gives:
mv2=mgl
Dividing both sides by m (assuming m≠0):
v2=gl
Taking the square root of both sides, we find:
v=√gl
Therefore, the minimum speed of the particle at its highest point must be:
v=√gl
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Single Correct
18 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Assertion And Reason
28 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A particle of mass m is attached to an end of a light rigid rod of length a. The other end of the rod is fixed, so that the rod can rotate freely in vertical plane about its fixed end. The mass m is given a horizontal velocity u at the lowest point. (a) Prove that when the radius to the mass makes an angle θ with the upward vertical the horizontal component of the acceleration of the mass (measured in direction of u) is [g(2+3cosθ)−u2/a]sinθ (b) If 4ag ltu2 lt5ag, show that there are four points at which horizontal component of acceleration is zero. locate the points.
View SolutionA point particle of mass M is attached to one end of a massless rigid non-conducting rod of length L. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges +q and −q respectively. This arrangement is held in a region of a uniform electric field E such that the rod makes a small angle θ (say of about 5 degree) with the field direction, fig. Find an expression for the minimum time needed for the rod to become parrallel to the field after it is set free.

View Solution
Knowledge Check
A particle of mass m is fixed to one end of a light rigid rod of length l and rotated in a vertical circular path about its other end. The minimum speed of the particle at its highest point must be
AzeroB√glC√1.5glD√2glA particle of mass m is fixed to me one end of a light right rod of length l and rotated in a vertical circular path about its other end. The minmum speed of the particle at its highest point must be
AzeroB√glC√1.5glD√2glA particle of mass m is tied to a light string of length l and rotated along a vertical circular path. What should be the minimum speed at the highest point of its path so that the string does not become slack at any position ?
A√2glB√glCzeroD√gl/2
A sphere of mass m is tied to end of a string of length l and rotated through the other end along a horizontal circular path with speed v . The work done in full horizontal circle is
View SolutionA mass m is attached to the end of a rod of length l. The mass goes along a vertical circular path with the other end, hinged at its centre . What should be the minimum speed of mass at the bottom of this circular path
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
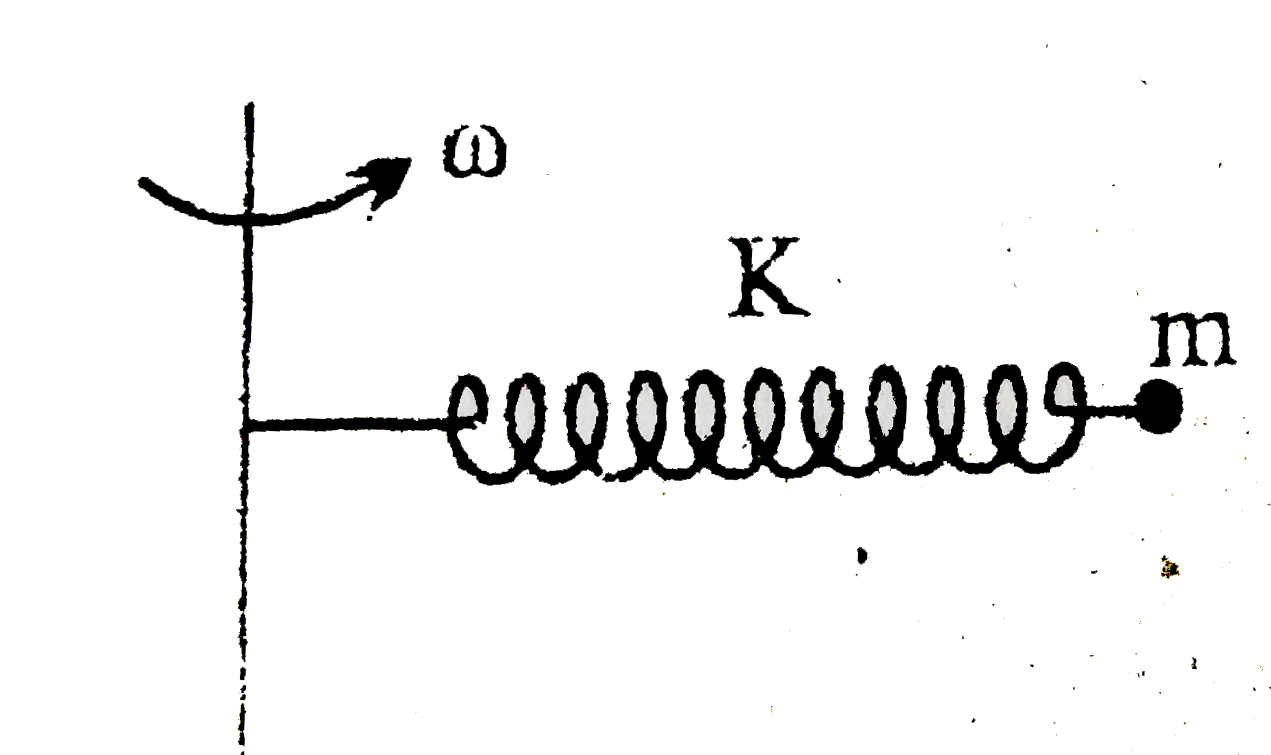
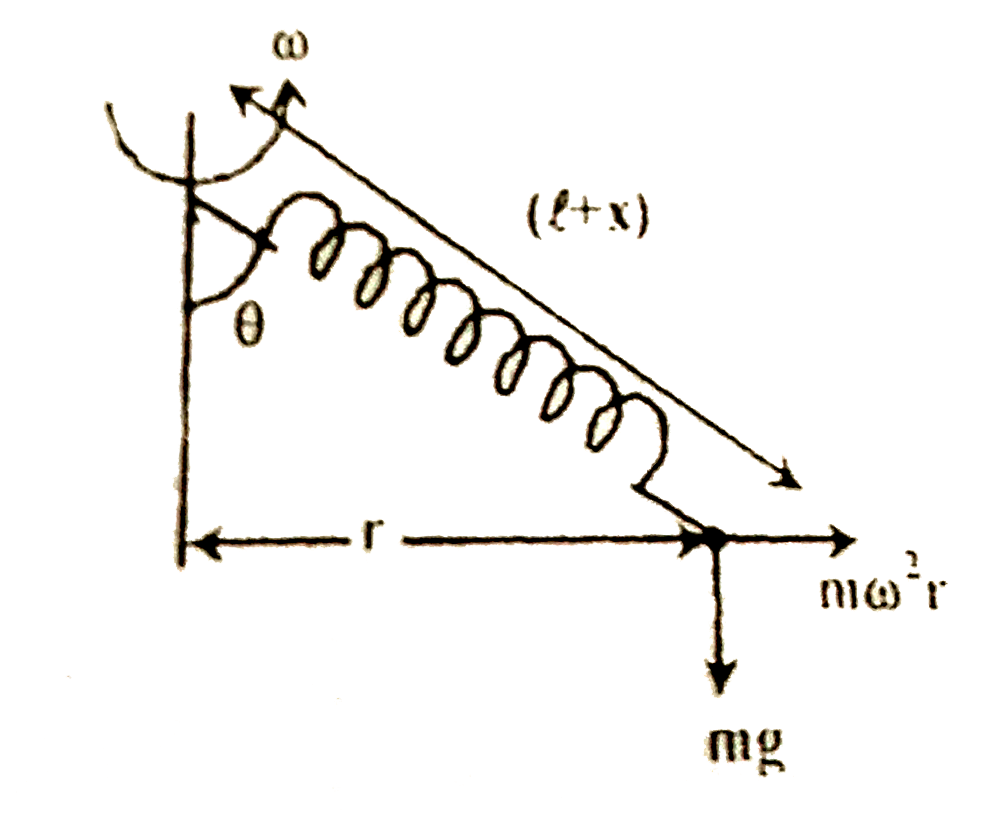
View SolutionA particle of mass m is fixed to one end of a light spring of force constant k and unstretched length l. The other end of the spring is fixed on a vertical axis which is rotaing with an angular velocity ω. The increase in length of th espring will be
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View Solution
