A particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
mω2tk
mω2lk+mω2
mω2lk−mω2
none of the above
The correct Answer is:C
Let dl be the increase in length of spring. It means the particle will move on a circular path of radius (l+dl) and the restoring force due to spring =(kdl) will provide the required centripetal force
∴mω2(l+dl)=kdl or dl=mω2lk−mω2
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - integer type question
8 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Assertion-Reason Type Questions
23 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question-II
14 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionAn underformed spring with the spring constant k has length l0. When the system (Fig.) rotates at an angular
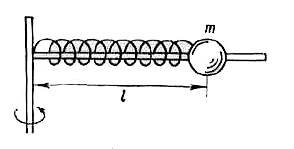
velocity ω, the weight with mass m causes an extension of the spring. Find the length l of the rotating spring.
View Solution
Knowledge Check
A particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
 Amω2lkBmω2lk−mω2Cmω2lk+mω2Dnone of these
Amω2lkBmω2lk−mω2Cmω2lk+mω2Dnone of theseA particle of mass m is fixed to one end of a light spring of force constant k and unstretched length l. The other end of the spring is fixed on a vertical axis which is rotaing with an angular velocity ω. The increase in length of th espring will be
 Amω2lkBmω2lk−mω2Cmω2lk+mω2DNone of these
Amω2lkBmω2lk−mω2Cmω2lk+mω2DNone of these
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. At the instant the speed of block is maximum the magitude of force exeted by the spring on the block isAmg2BmgCzeroDnone of these

A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. Till the blocks reaches its lowest position for the first time, the time duration for which the spring remains compressed is
View Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. As the block is coming down, the maximum speed attained by the block is
View SolutionA block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionA massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
View SolutionA body of mass m is suspended from a massless spring of natural length l. It stretches the spring through a vertical distance y. The potential energy of the stretched spring is
View Solution