A particle of mass m is moving with a constant speed v in a circular path in a smooth horizontal plate (plan of the paper ) by a spring force as shown in figure If the natural length of the spring is l0 and stiffeness of the spring is k find the elongation of the spring

If the particle executes uniform circular motion , its speeds must be uniform because there is no tangential force to speed it up . Here the spring force kt acting on the particlein the centripetal force caused by the elongation x of the spring
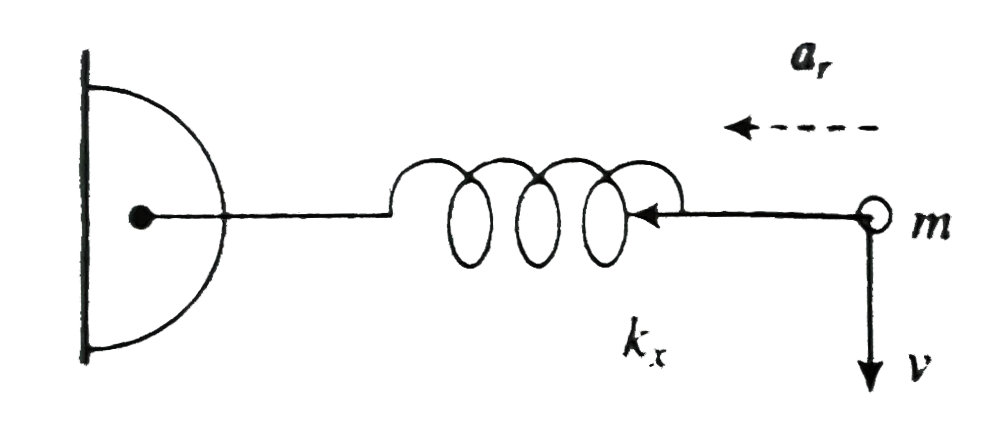
Equation of motion
∑Fr=FSP=mar
But centripental acceleration
ar=v2R (where R= radius of circular path)
Radius os rotation R=10+x
|FSP|=kx
Put in (i)kx=mv2(10+x)⇒kx2+kl0x−mv2=0
This given x=√k2120+4mv2k−kl02k
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Block of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution
Knowledge Check
A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2A bob of mass m is connected to a spring of spring constant k and a string which is fixed to the ceiling as shown in figure. Original length of the spring is L and the bob rotates in a horizontal circle centred at the fixed rod. Assuming the spring remains horizontal, then elongation in the spring is :
 A(mg−mω2L)tanθmω2+kBmgtanθ+mω2Lmω2−kCmgtanθ+mω2LkDgtanθ−ω2Lω2−k/m
A(mg−mω2L)tanθmω2+kBmgtanθ+mω2Lmω2−kCmgtanθ+mω2LkDgtanθ−ω2Lω2−k/mIf the system is suspended by the mass m the length of the spring is l1. If it is inverted and hung by mass M, the length of the spring is l2. Find the natural length of the spring.
 Aml1+Ml2m+MBml2+Ml1m+MCml1−Ml2m−MDml2−Ml1m−M
Aml1+Ml2m+MBml2+Ml1m+MCml1−Ml2m−MDml2−Ml1m−M
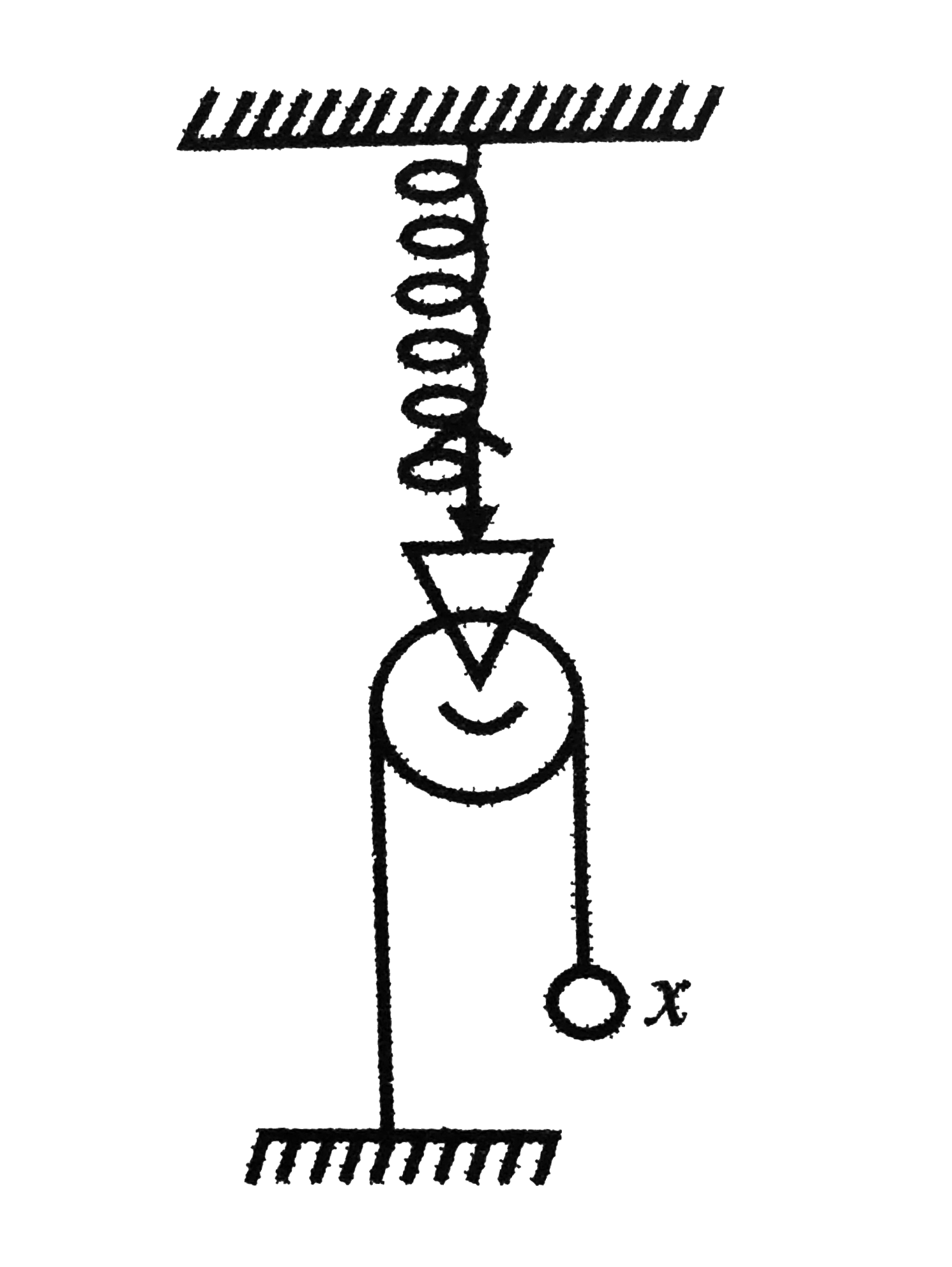
A body of mass m hangs by an inextensible string that passes over a smooth mass less pulley that is fitted with a light spring of stiffness k as shown in figure. If the body is released from rest and the spring is released, calculate the maximum elongation of the spring.
View SolutionA rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
View SolutionThe system of the wedge and the block connected by a massless spring as shown in the figure is released with the spring in its natural length. Friction is absent. Maximum elongation in the spring will be
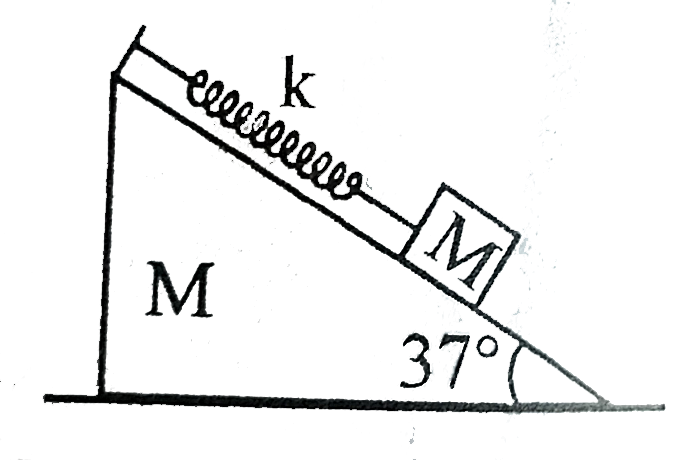
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View Solution
