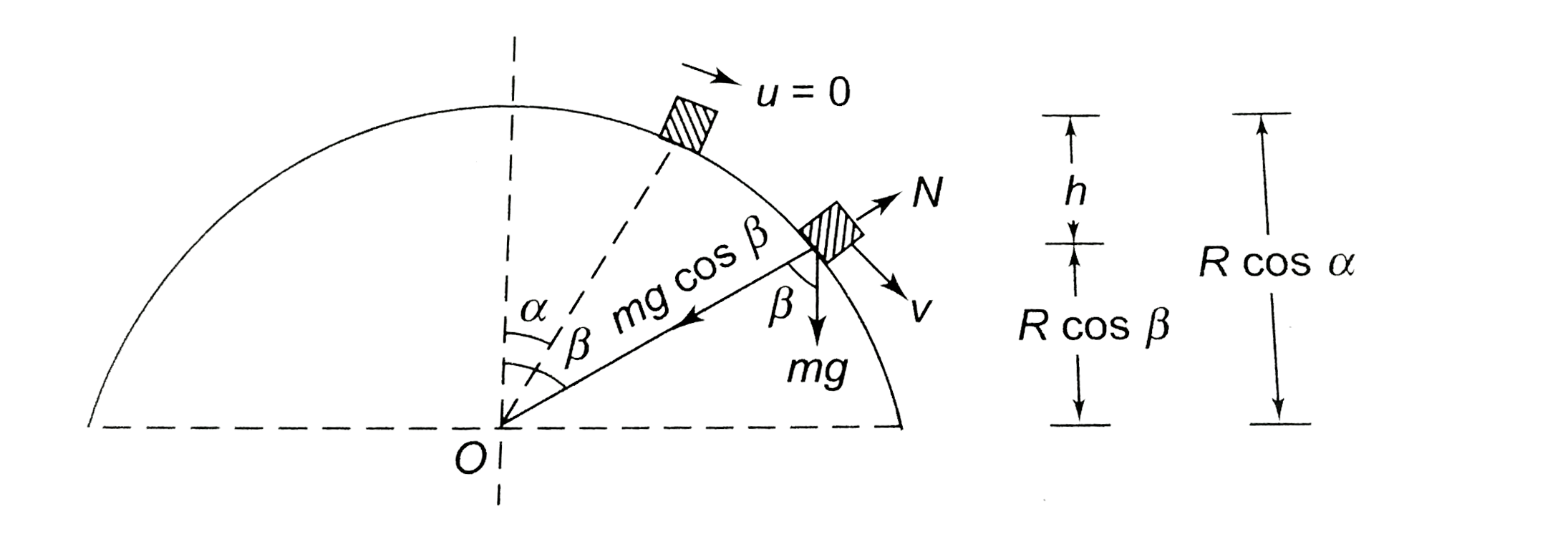
A particle of mass m is released on a fixed. Smooth sphere of radius R at a position, where the radius through the particle makes an angle of α with the verticle. What is the angle made by radius through the particle when the particle loses contact with sphere? (cosα=3/4)
h=R(cosα−cosβ)
v2=u2+2gh=0+2gR(cosα−cosβ)
mgcosβ−N=mv2R
when the particle loses contact
N=0
v2=gRcosβ=2gR(cosα−cosβ)
3cosβ=2cosα=2×34
cosβ=12⇒β=60∘
Topper's Solved these Questions
Similar Questions
A particle of mass m is kept on a fixed , smooth sphere of radius R at a position, where the rdius thrugh the particle makes an angle of 300 with the vertical. The particle is releases from this positon. a. What is the force exerted by the sphere on teh particle just after the release? b. Find the distance travelled by the particle before it leaves contact with the sphere.
View SolutionA small box of mass m is kept on a fixed, smooth sphere of radius R at a position where the radius through the box makes an angle of 30∘ with the vertical. The box is released from this position
(a) What is the force exerted by the sphere on the box just after the release ?
(b) Find the distance travelled by the box before it leaves contact with the sphere.
View Solution
Knowledge Check
A particle of mass m begins to slide down on a fixed smooth sphere from the top, when it breaks off the sphere, the tangential accleration will be
A2g/3BgC√53gDg2A particle of mass m is released from the edge of a rough bowl of radius r. It momentrially comes to rest at point B, whose radius vector making an angle 30∘ with the vertical . If μ=1√3, then work done by the frictional force on the particle is
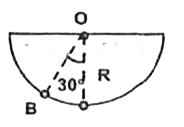 A−μmgR2BmgR2C−√3μmgR2D−√3mgR2
A−μmgR2BmgR2C−√3μmgR2D−√3mgR2A particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
Ait will start moving along a circular path if v<√gRBit will start moving along a circular path if v>√gRCit will start moving along a parabolic path if v<√gRDit will start moving along a parabolic path if v>√gR
A small box of mass m is placed on the outer surface of a smooth fixed sphere of radius R at a point where the radius makes a angle Pse with the vertical. The box is released from this position. Find the distance travelled by the box before it leaves contact with the sphere.
View SolutionA particle of mass m being to slide down a fixed smooth sphere from the top as shown. If its acceleration when it breaks off the sphere is 2a. The value of a is :
View SolutionA particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.

View Solution