A particle of mass m is suspended by a string of length l from a fixed rigid support. A sufficient horizontal velocity =√3gl is imparted to it suddenly. Calculate the angle made by the string with the vertical when the accekleration of the particle is inclined to the string by 45∘ .
The correct Answer is:A, B
h=l(l−cosθ)
v^(2)v20−2gh=3gl−2gl(l−cosθ)=gl(1+2cosθ)
At 45∘ means radial and tangential components of acceleration are equal.
:. v2l=gsinθ
or 1+2cosθ=sinθ
Solving the equation we get, θ=90∘orπ2
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A particle of mass m is suspended by a string of length l from a fixed rigid support. Particle is imparted a horizontal velocity u=√2gl. Find the angle made by the string with the vertical when the acceleration of the particle is inclined to the string by 45∘?
View SolutionA particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from the position as shown in Fig. Calculate
a. the impulse developed in the string when it becomes taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
View Solution
Knowledge Check
A particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
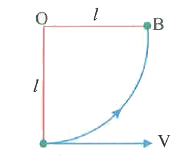 Av=√2glBv=√3glCv=√glDv=2gl
Av=√2glBv=√3glCv=√glDv=2glA smalll bob attached to a string of length l is suspended from a rigid support and rotates with uniform speed along a circle in a horizontal plane. Let θ be the angle made by the string with the vertical, then the length of a simple pendulum having the same period is
Al/cosθBlsinθCl/sinθDlcosθAn iron ball of mass m, suspended by a light inextensible string of length l from a fixed point O, is shifted by θ0 as shown so as to strike the vertical wail perpendicularly.The maximum angle made by the string with vertical after the first collision, if e is the coefficient of restitution, is
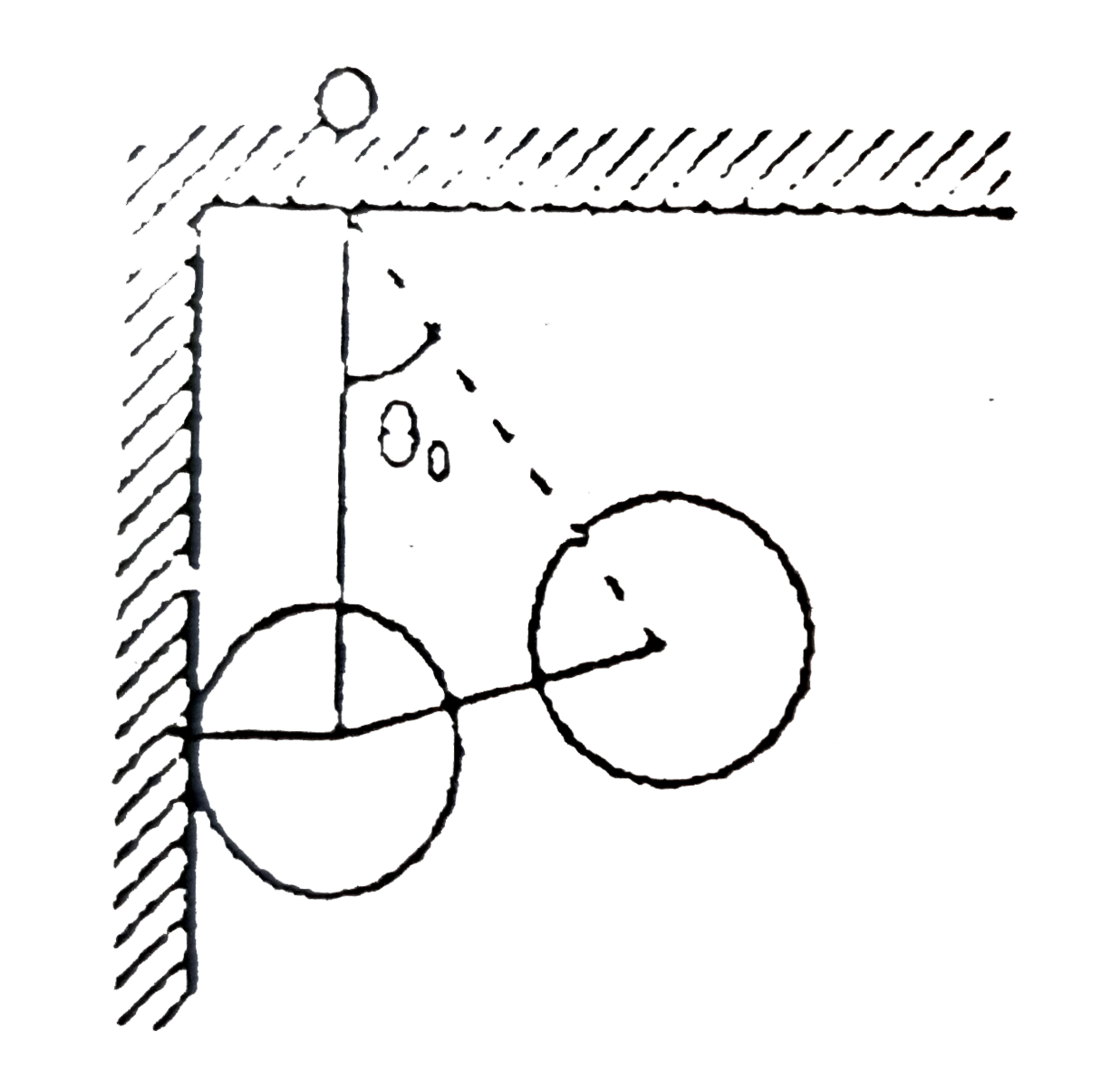 Asin−1{1−e2(1−cosθ0)}Bcos−1{1−e2(1−cosθ0)}Ctan−1{1−e2(1−cosθ0)}Dzero
Asin−1{1−e2(1−cosθ0)}Bcos−1{1−e2(1−cosθ0)}Ctan−1{1−e2(1−cosθ0)}Dzero
A particle is suspended by a light vertical inelastic string of length 1 from a fixed support. At its equilbrium position it is projected horizontally with a speed √6gl. Find the ratio of the tension in the string in its horizontal position to that in the string when the particle is vertically above the point of support.
View SolutionA bob of mass m suspended by a light inextensible string of length 'l' from a fixed point. The bob is given a speed of √6gl. Find the tension in the string when string deflects through an angle 120∘ from the vertical.
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
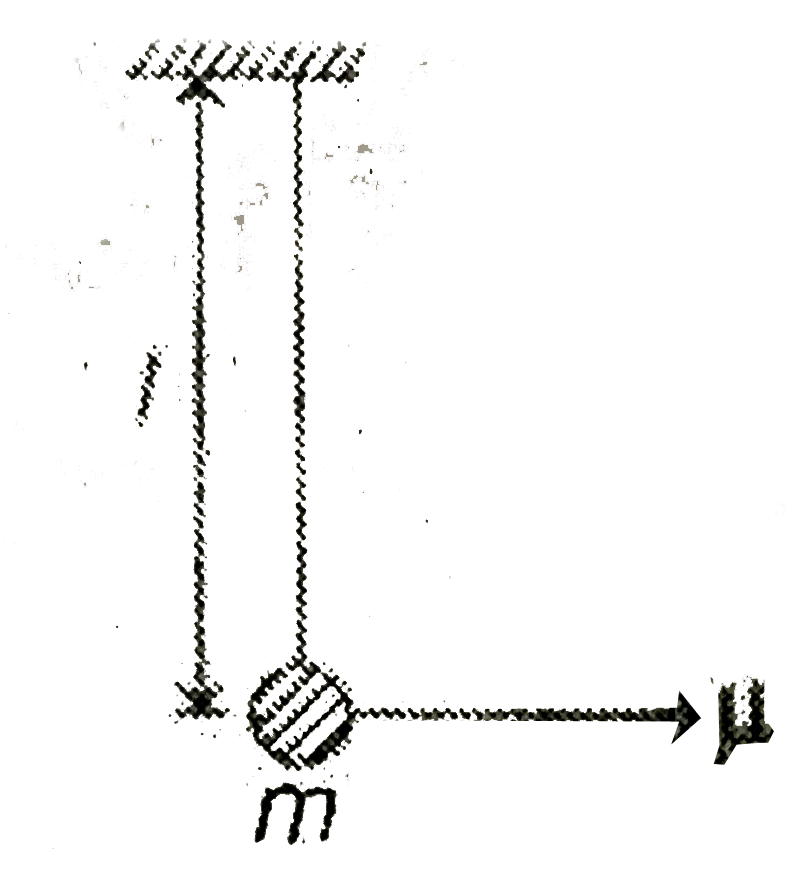
The tension in the string at an instant when acceleration of the particle is horizontal and √3g is
View Solution
