A heavy partile slides under gravity download the inside of a smooth vertical tube dheld in vertical plane. It starts from the highest point with velocity √2ag , where a is the radius of the circle. Find the angular position θ (as shown in figure) at which the vertical acceleration of the particle is maximum.
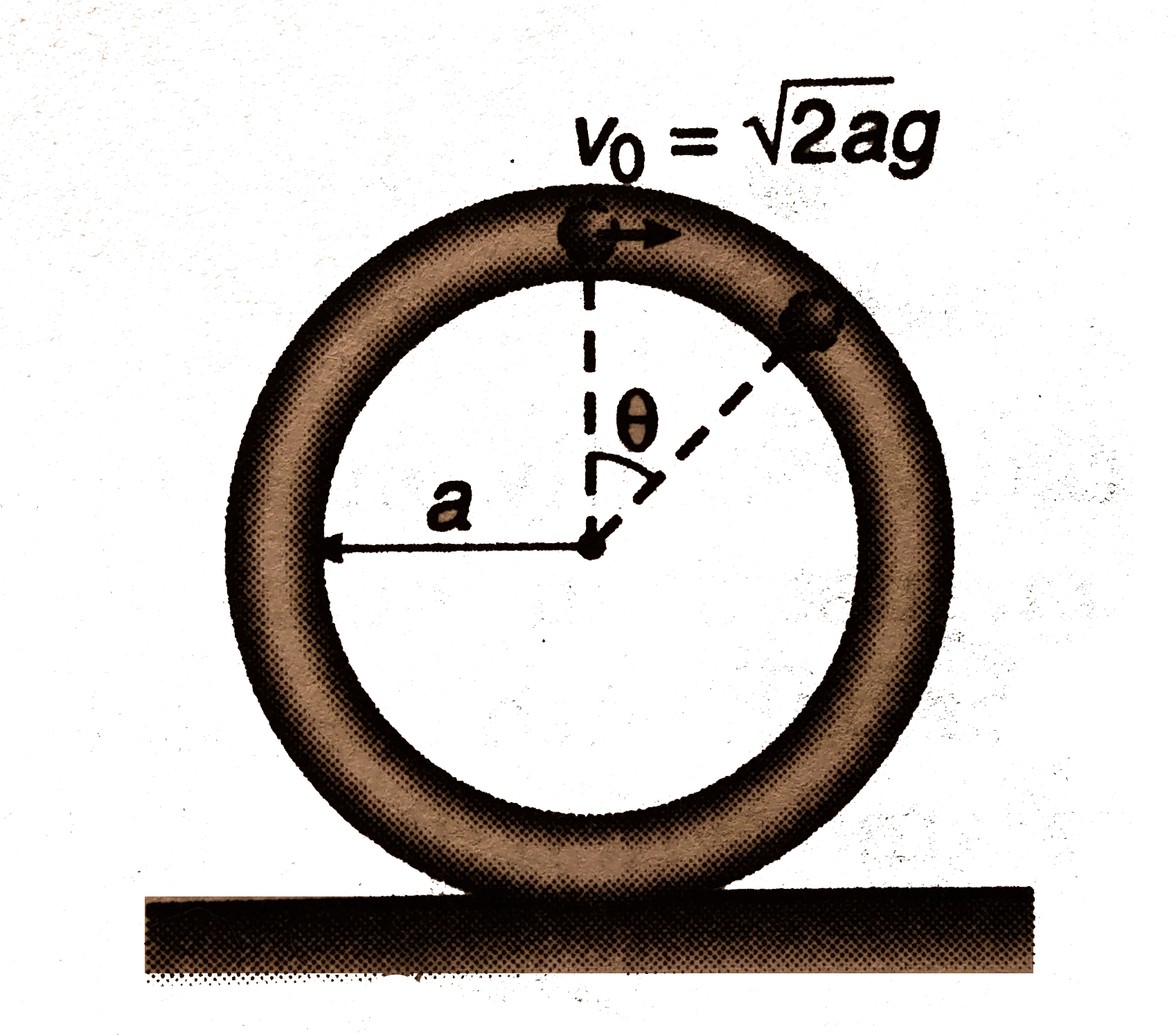
A heavy partile slides under gravity download the inside of a smooth vertical tube dheld in vertical plane. It starts from the highest point with velocity sqrt(2ag) , where a is the radius of the circle. Find the angular position theta (as shown in figure) at which the vertical acceleration of the particle is maximum.

Text Solution
Verified by Experts

The correct Answer is:A, B, C

At position θ ,
v2=v20+2gh
where, h=a(1−cosθ)
:. v2=(√2ag)2+2ag(1−cosθ)
or v2=2ag(2−cosθ) ...(i)
N+mgcosθ=mv2a
or N+mgcosθ=2mg(2−cosθ)
or N=mg(4−3cosθ)
Net vertical force,
F=Ncosθ+mg
=mg(4cosθ−3cos2θ+1)
This force (or acceleration) will maximum when dFdthη=0
or −4sinθ+6sinθcos=0
So, either
sinθ=0 ,
θ=0∘ ,
or cosθ=23 ,
θ=cos−1(23)
θ=0∘ is unacceptable
Therefore, the desired position is at
θcos−1(23)

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 11PHYSICSCIRCULAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A particle is projected vertically upwards with a velocity √gR, where R denotes the radius of the earth and g the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is

    AR2
    BR
    C2R
    D5R4

  • A particle tied to a string describes a vertical circular motion of radius r continually. If it has a velocity √3gr at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is

    A1:6
    B1:4
    C1:3
    D1:2

  • A particle is projected under gravity with velocity √2ag from a point at a height h above the level plane at an angle θ to it. The maximum range R on the grond is :

    A√(a2+1)/h
    B√(a2h)
    C√(ah)
    D2√a(a+h)