A particle of mass m rests on a horizontal floor with which it has a coefficient of static friction . It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has to be applied.
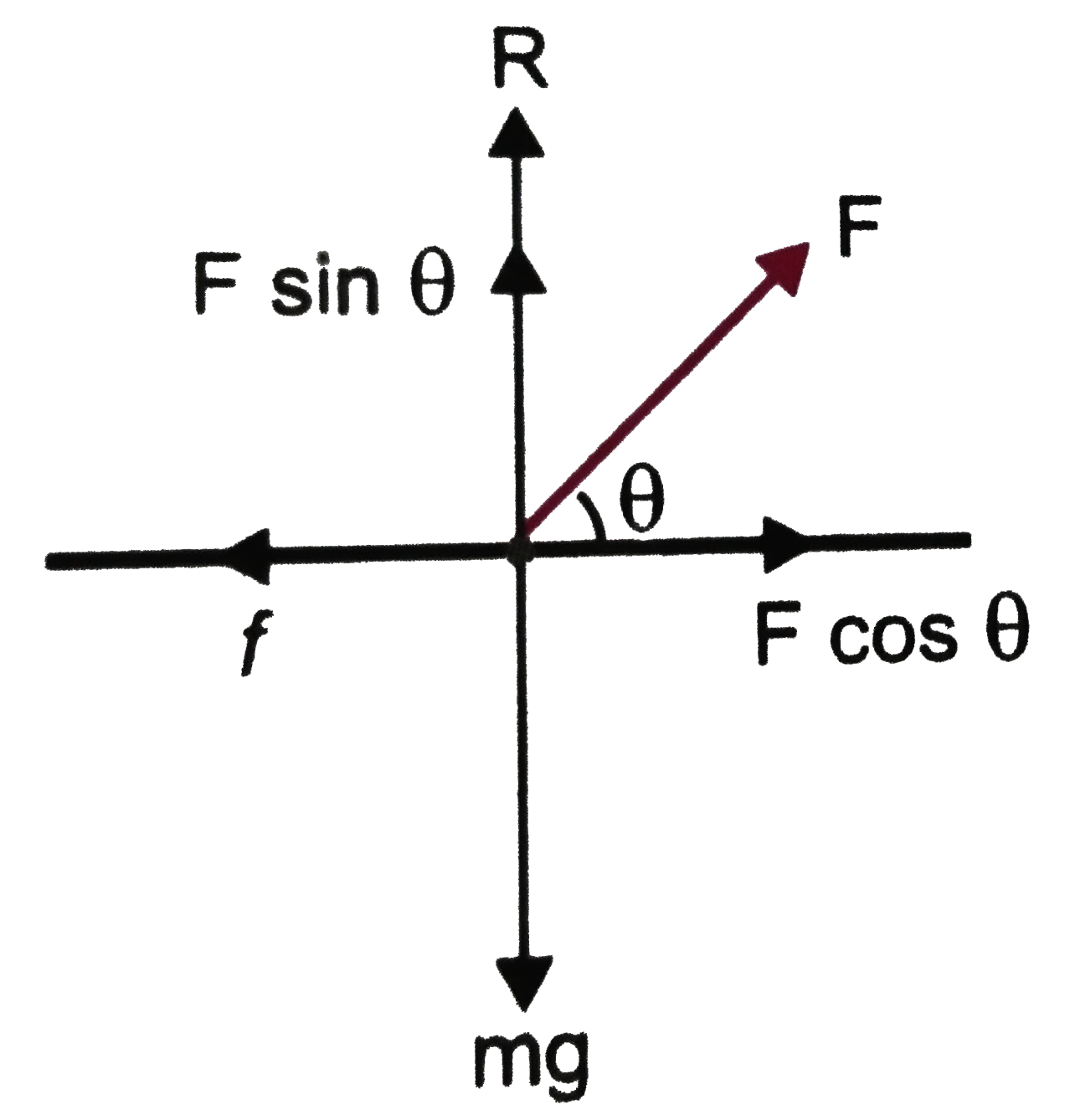
Let a force F be applied at to move the body , as shown in Here , f represents the force of friction
For horizontal equilibrium ,
put in (i)
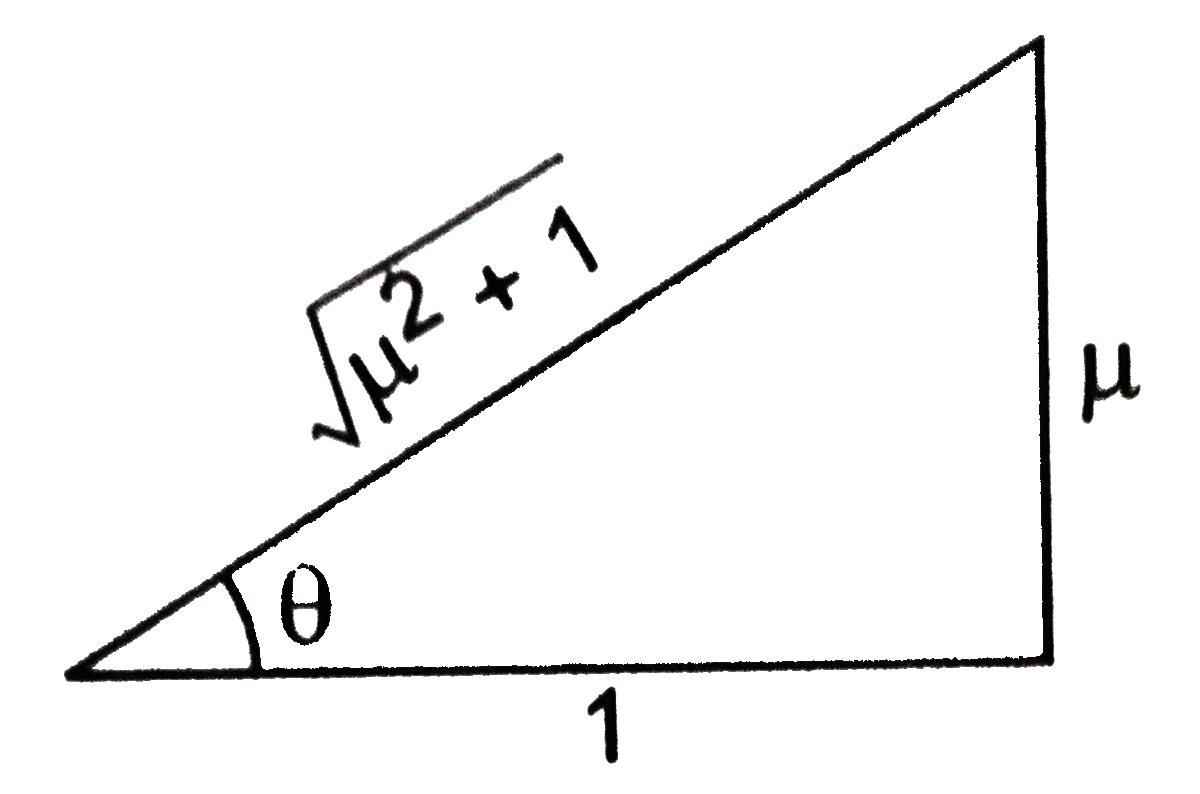
Now , F will be minimum , when denominator ,
= maximum
or
put in (iii) ,
This is the direction of F min
 .
.
Similar Questions
A blocky of mass m rests on a horizotal floor with which it has a coefficient of static friction μ. It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has be applies.
View SolutionA body of mass 1 kg rests on a horizontal floor with which it has a coefficient of static friction 1√3. It is desired to make the body move by applying the minimum possible force FN. The value of F will be ________. (Round off to the Nearest Integer)
[Take g=10ms−2]
View Solution
Knowledge Check
A blocky of mass m rests on a horizotal floor with which it has a coefficient of static friction μ. It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has be applies.
AμmgB√1+μ2μmgCμ√1+μ2mgDμmg√1+μ2An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is -
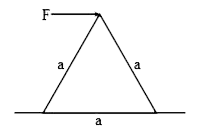 Amg√3Bmg4Cμmg√3Dμmg4
Amg√3Bmg4Cμmg√3Dμmg4An equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
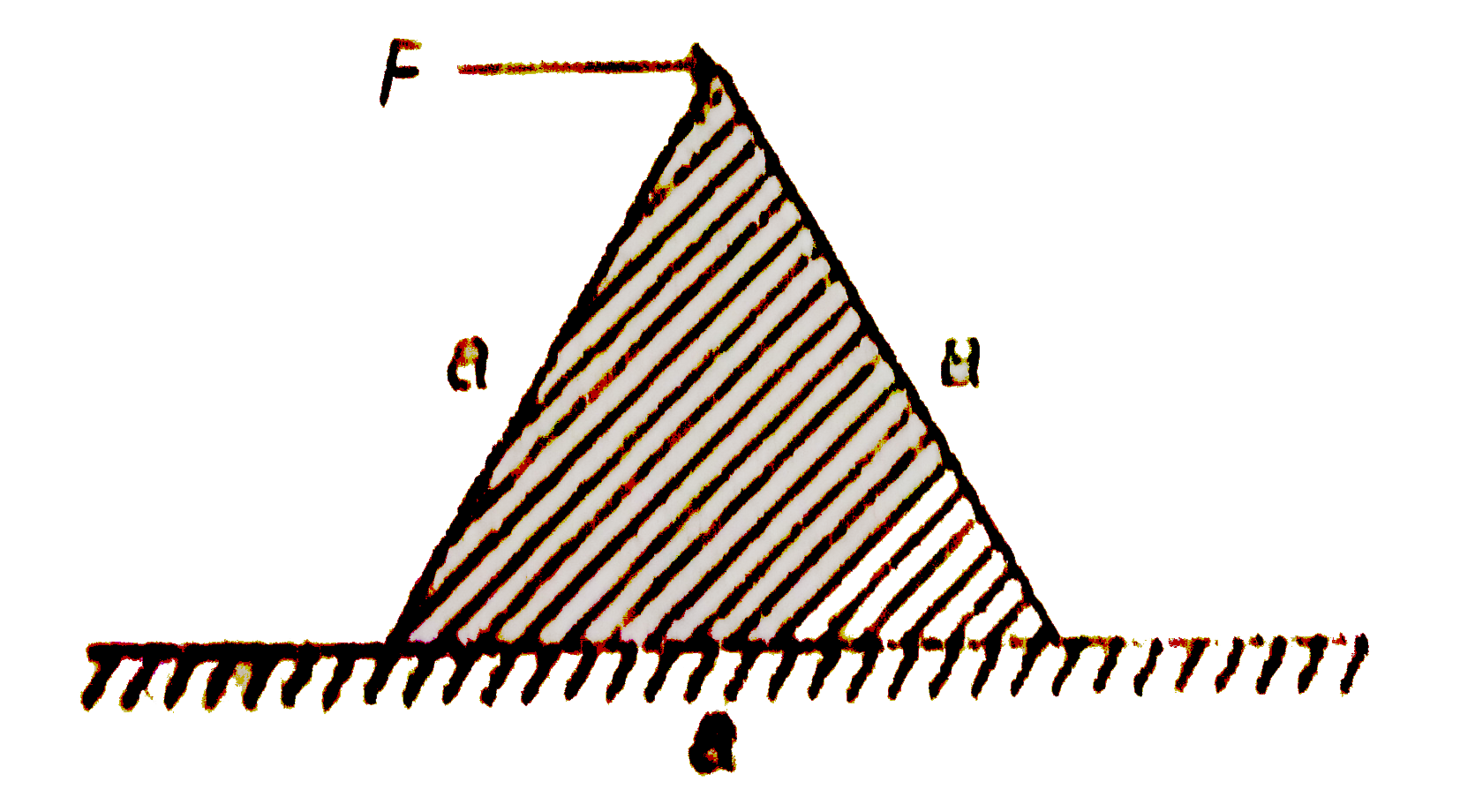 A(mg)(√3)Bmg4Cμmg√3Dμmg4
A(mg)(√3)Bmg4Cμmg√3Dμmg4
A body of mass m rests on a horizontal rough platform. Coefficient of static friction is u. Calculate the minimum possible force required to move the body along the platform.
View SolutionA block of mass m rests on a horizontal floor for which coefficient of friction is μ . Find the magnitude and the direction of force that should be applied to just move the block so that the applied force is minimum.
View SolutionA train starting from rest is moving along a straight track with a constant acceleration fo 2.5m/s2. A passenger at rest in the train observes a particle of mass 2kg to be at rest on the floor with which it has a coefficient of friction μs=μk=0.5 .Six seconds after the starting of the train , a horizontal force F = 13N is applied to the particle for two seconds duration. The passenger now observes the particle to move perpendicular to the direction of the train.
(a) calculate the kinetic energy of the particle with respect to the passenger at the end of 8 seconds after starting of the train.
( b) repeat the calculate of ( a) for an observer on the ground.
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View Solution