A particle of mass m0, travelling at speed v0. Strikes a stationary particle of mass 2m0. As a result of the particle of mass m0 is deflected through 45∘ and has a final speed of v0√2. Then the speed of the particle of mass 2m0 after this collision is
(a) v02
(b) v02√2
(c) √2v0
(d) v0√2
The correct Answer is:B
To solve the problem, we will use the principle of conservation of linear momentum. Let's break it down step by step.
Step 1: Identify the initial momentum
Before the collision, we have:
- The momentum of the particle of mass m0 moving with speed v0:
Initial momentum of m0=m0v0
- The stationary particle of mass 2m0 has no momentum:
Initial momentum of 2m0=0
Thus, the total initial momentum Pinitial is:
Pinitial=m0v0+0=m0v0
Step 2: Identify the final momentum
After the collision:
- The particle of mass m0 is deflected at an angle of 45∘ with a final speed of v0√2. We can resolve this velocity into its components:
- vx1=v0√2cos(45∘)=v0√2⋅1√2=v02
- vy1=v0√2sin(45∘)=v0√2⋅1√2=v02
Thus, the final momentum of the particle of mass m0 is:
Final momentum of m0=m0(v02^i+v02^j)
Let the velocity of the particle of mass 2m0 after the collision be →V=Vx^i+Vy^j. The final momentum of the particle of mass 2m0 is:
Final momentum of 2m0=2m0→V
Step 3: Apply conservation of momentum
According to the conservation of momentum:
Pinitial=Pfinal
This gives us:
m0v0=m0(v02^i+v02^j)+2m0→V
Step 4: Separate into components
Separating into ^i and ^j components, we have:
1. For the ^i component:
m0v0=m0v02+2m0Vx
Simplifying gives:
v0=v02+2Vx⟹2Vx=v02⟹Vx=v04
2. For the ^j component:
0=m0v02+2m0Vy
Simplifying gives:
0=v02+2Vy⟹2Vy=−v02⟹Vy=−v04
Step 5: Calculate the magnitude of velocity →V
Now we have:
→V=v04^i−v04^j
The magnitude of →V is:
|→V|=√(v04)2+(−v04)2=√v2016+v2016=√2v2016=√v208=v02√2
Final Answer
Thus, the speed of the particle of mass 2m0 after the collision is:
v02√2
---
Before the collision, we have:
- The momentum of the particle of mass m0 moving with speed v0:
Initial momentum of m0=m0v0
- The stationary particle of mass 2m0 has no momentum:
Initial momentum of 2m0=0
Pinitial=m0v0+0=m0v0
After the collision:
- The particle of mass m0 is deflected at an angle of 45∘ with a final speed of v0√2. We can resolve this velocity into its components:
- vx1=v0√2cos(45∘)=v0√2⋅1√2=v02
- vy1=v0√2sin(45∘)=v0√2⋅1√2=v02
Final momentum of m0=m0(v02^i+v02^j)
Final momentum of 2m0=2m0→V
According to the conservation of momentum:
Pinitial=Pfinal
This gives us:
m0v0=m0(v02^i+v02^j)+2m0→V
Separating into ^i and ^j components, we have:
1. For the ^i component:
m0v0=m0v02+2m0Vx
Simplifying gives:
v0=v02+2Vx⟹2Vx=v02⟹Vx=v04
0=m0v02+2m0Vy
Simplifying gives:
0=v02+2Vy⟹2Vy=−v02⟹Vy=−v04
Now we have:
→V=v04^i−v04^j
|→V|=√(v04)2+(−v04)2=√v2016+v2016=√2v2016=√v208=v02√2
Thus, the speed of the particle of mass 2m0 after the collision is:
v02√2
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Single Correct Option
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 More Than One Correct
8 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A particle of mass m, moving with velocity v collides a stationary particle of mass 2m. As a result of collision, the particle of mass m deviates by 45∘ and has final speed of v2. For this situation mark out the correct statement (s).
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA particle of mass m moving with velocity v strikes a stationary particle of mass 2m and sticks to it. The speed of the system will be.
A. v2
B. 2v
C. v3
D. 3v
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
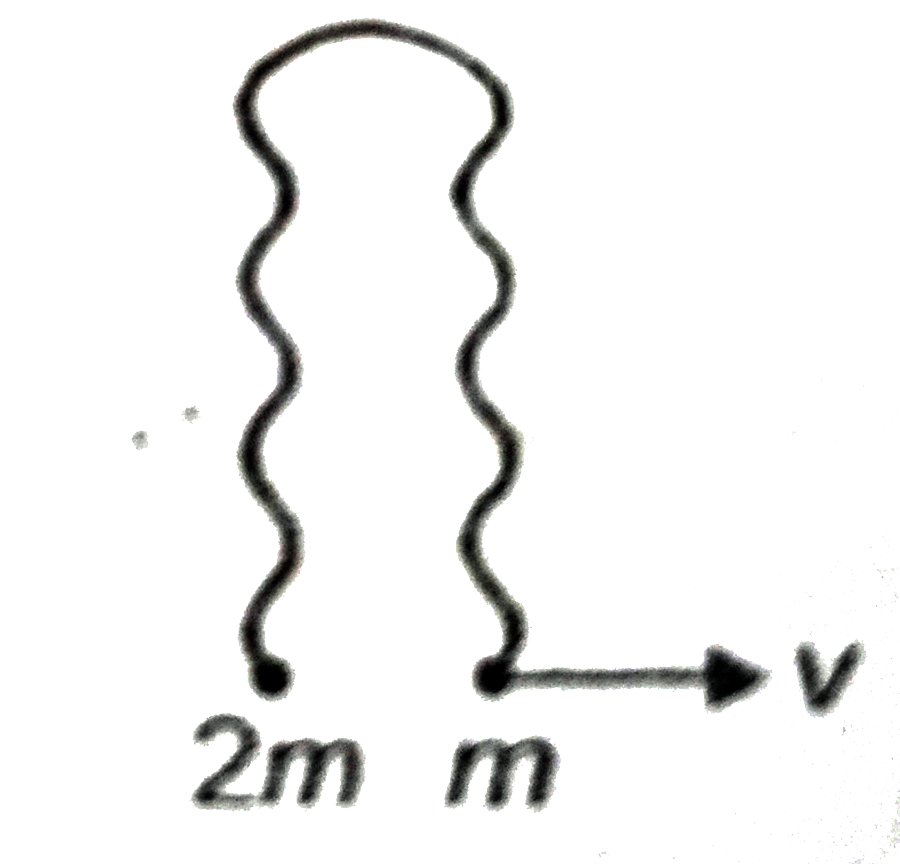
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.

View SolutionA particle of mass m moving towards west with speed v collides with another particle of mass m movies towards south. If two particles st ich t o each other the speed of the new particle of mass 2 m will be
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View Solution
