A particle of mass m moving towards west with speed v collides with another particle of mass m movies towards south. If two particles st ich t o each other the speed of the new particle of mass 2 m will be
v√2
v√2
v/2
v
The correct Answer is:B
To solve the problem, we need to analyze the collision of two particles and apply the principles of conservation of momentum. Let's go through the solution step by step.
Step 1: Understand the scenario
We have two particles, each of mass m:
- Particle 1 is moving towards the west with speed v.
- Particle 2 is moving towards the south with speed v.
When they collide, they stick together, forming a new particle with mass 2m.
Step 2: Set up the coordinate system
Let's establish a coordinate system:
- The west direction is negative x-axis.
- The south direction is negative y-axis.
Step 3: Write down the initial momentum
The momentum of each particle before the collision can be expressed as:
- For Particle 1 (moving west):
p1x=−mv(x component)
p1y=0(y component)
- For Particle 2 (moving south):
p2x=0(x component)
p2y=−mv(y component)
Step 4: Calculate total initial momentum
The total initial momentum in the x-direction and y-direction is:
- Total momentum in x-direction:
pinitial,x=p1x+p2x=−mv+0=−mv
- Total momentum in y-direction:
pinitial,y=p1y+p2y=0−mv=−mv
Step 5: Write down the final momentum after collision
After the collision, the two particles stick together and move with a speed V at an angle θ with respect to the negative y-axis. The momentum components of the combined mass 2m are:
- In the x-direction:
pfinal,x=−2mVcos(θ)
- In the y-direction:
pfinal,y=−2mVsin(θ)
Step 6: Apply conservation of momentum
According to the conservation of momentum:
- In the x-direction:
−mv=−2mVcos(θ)
Simplifying gives:
v=2Vcos(θ)(1)
- In the y-direction:
−mv=−2mVsin(θ)
Simplifying gives:
v=2Vsin(θ)(2)
Step 7: Divide the equations to find θ
Dividing equation (1) by equation (2):
vv=2Vcos(θ)2Vsin(θ)
This simplifies to:
1=cos(θ)sin(θ)⇒tan(θ)=1
Thus,
θ=45∘
Step 8: Substitute θ back to find V
Substituting θ=45∘ into equation (1):
v=2Vcos(45∘)
Since cos(45∘)=1√2:
v=2V⋅1√2⇒v=2V√2⇒v=√2V
Thus,
V=v√2
Final Answer
The speed of the new particle of mass 2m after the collision is:
V=v√2
We have two particles, each of mass m:
- Particle 1 is moving towards the west with speed v.
- Particle 2 is moving towards the south with speed v.
Let's establish a coordinate system:
- The west direction is negative x-axis.
- The south direction is negative y-axis.
The momentum of each particle before the collision can be expressed as:
- For Particle 1 (moving west):
p1x=−mv(x component)
p1y=0(y component)
p2x=0(x component)
p2y=−mv(y component)
The total initial momentum in the x-direction and y-direction is:
- Total momentum in x-direction:
pinitial,x=p1x+p2x=−mv+0=−mv
pinitial,y=p1y+p2y=0−mv=−mv
After the collision, the two particles stick together and move with a speed V at an angle θ with respect to the negative y-axis. The momentum components of the combined mass 2m are:
- In the x-direction:
pfinal,x=−2mVcos(θ)
pfinal,y=−2mVsin(θ)
According to the conservation of momentum:
- In the x-direction:
−mv=−2mVcos(θ)
Simplifying gives:
v=2Vcos(θ)(1)
−mv=−2mVsin(θ)
Simplifying gives:
v=2Vsin(θ)(2)
Dividing equation (1) by equation (2):
vv=2Vcos(θ)2Vsin(θ)
This simplifies to:
1=cos(θ)sin(θ)⇒tan(θ)=1
Thus,
θ=45∘
Substituting θ=45∘ into equation (1):
v=2Vcos(45∘)
Since cos(45∘)=1√2:
v=2V⋅1√2⇒v=2V√2⇒v=√2V
Thus,
V=v√2
The speed of the new particle of mass 2m after the collision is:
V=v√2
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
45 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)
16 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle of mass m moving eastward with a velocity V collides with another particle of same mass moving northwards with the same speed V. The two particles coalesce and the new particle moves in NE direction. Calculate magnitude and direction of velocity of new particle.
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
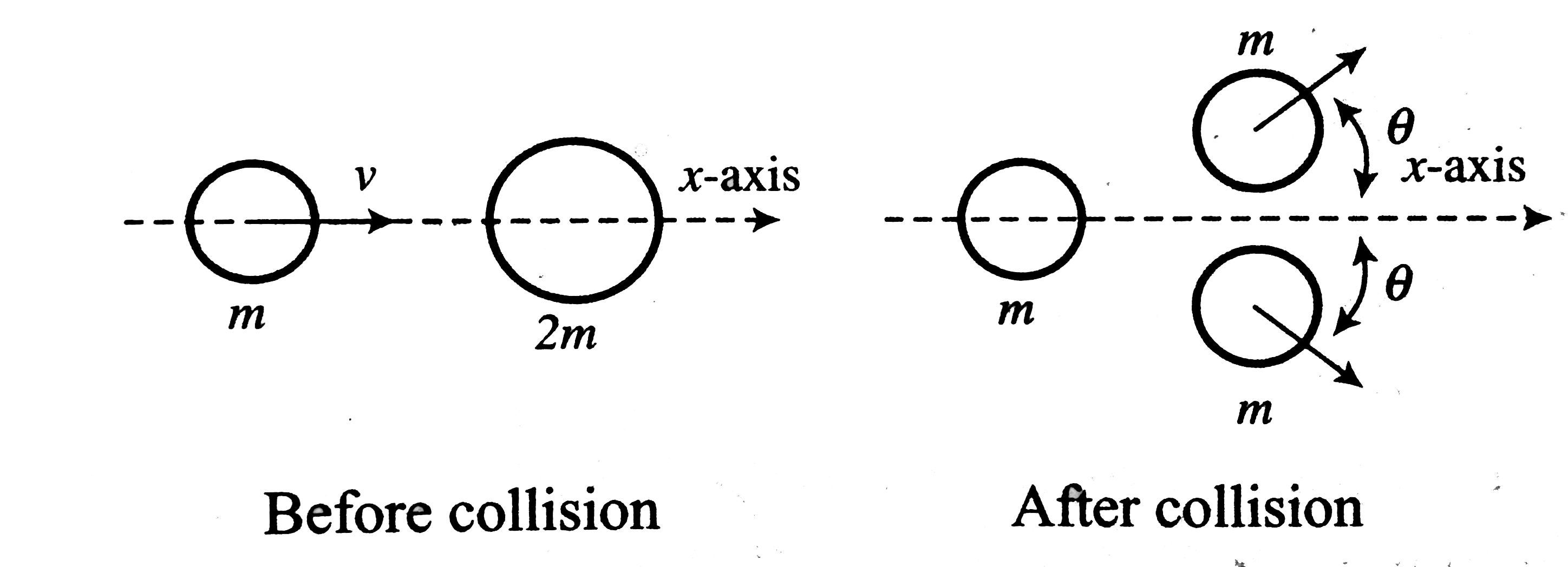
View SolutionA particle of mass m is moving along the x-axis with speed v when It collides with a particle of mass 2m initially at rest. After the collision, the first particle has come to rest and the second particle has split into two equal-mass pieces that are shown in the figure. Which of the following statements correctly describes the speeds of the two places? (θ>0)
View SolutionA particle of mass m with an initial velocity uˆi+2uˆj collides with a particle of mass 3m at rest. After collision, the two particles stick together and the combined particle moves with a velocity vˆi+v'ˆj. Which of the following is incorrect?
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m travelling with velocity v and kinetic energy E collides elastically to another particle of mass nm, at rest. What is the fraction of total energy retained by the particle of mass m?
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
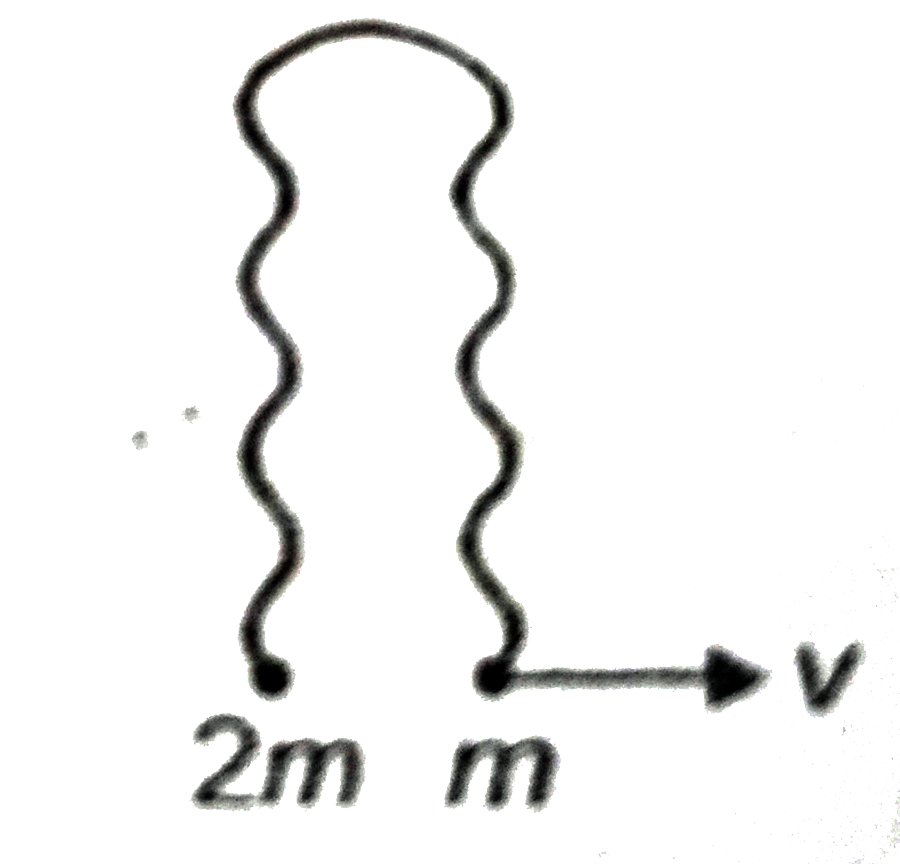
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
View Solution
