A particle of unit mass undergoes one -dimensional motion such that its velocity varies according to v(x)=βx−2nwhere βand n are constants and x is the position of the particle.The acceleration of the particle as a function of x, is given by:Solution in Tamil
−2nβ2x−4n−1
−2nβ2x−2n+1
−2nβ2e−4n+1
−2nβ2x−2n−1
Step by step video & image solution for A particle of unit mass undergoes one -dimensional motion such that its velocity varies according to v(x)=betax^(-2n)where betaand n are constants and x is the position of the particle.The acceleration of the particle as a function of x, is given by: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
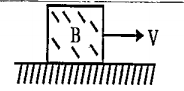
A block B is pushed momentarily along a horizontal surface with an initial velocity v. If μ is the coefficient of sliding friction betweenB and the surface , block B will come to rest after a time.
 .02:40View Solution
.02:40View SolutionThe phase difference between the instantaneous velocity & acceleration of a particle executing simple harmonic motion is
05:22View SolutionA particle of unit mass undergoes one-dimensional motion such that its velocity varies according to
v(x)=βx−2n
where β and n are constant and x is the position of the particle. The acceleration of the particle as a function of x is given by.04:35View Solutionएकांक द्रव्यमान का कोई कण एक विमीय गति करता है ओर इसका वेग समीकरण v(x)=bx−2n के अनुसार परिवर्तित होता है, जहाँ b तथा n स्थिरांक हैं तथा x कण कि स्थिति है। इस कण के त्वरण को x के फलन के रूप में निरूपित किया जा सकता है :
03:27View Solutionएकांक द्रव्यमान का कोई कण एकविमीय गति करता है और इसका वेग समीकरण v(x)=βx−2n के अनुसार परिवर्तित होता है, जहाँ β और n नियतांक हैं तहत x कण की स्थिति है। इस कण के त्वरण को x के फलन के रूप में निरूपित किया जा सकता है -
03:00View Solutionএকক ভরের একটি কণার একমাত্রিক গতিতে কণাটির বেগ v(x)=bx−2n সম্পর্ক অনুযায়ী পরিবর্তিত হয়, যেখানে b ও n হল ধ্রুবক এবং x হল কণাটির অবস্থান। x-এর অপেক্ষক হিসেবে কণাটির ত্বরণকে প্রকাশ করলে পাওয়া যায়
01:56View SolutionA particle of unit mass undergoes one-dimensional motion such that its velocity varies according to v (x) = beta x^(-2n) , where beta and n are constants and x is the position of the particle. The acceleration of the particle as a function of x is given by
03:46View Solution" If the velocity v of a particle varies as the square of its displacement "x" then the acceleration varies as "
02:01View SolutionThe displacement x of a particle varies with time as x=aeαt+beβt where a,b,a, β are constants and are positives. The velocity of the particle will:
05:22View SolutionA particle of unit mass undergoes one dimensional motion such that its velocity varies according to v(x) = = beta x ^(-2n) where B and n are constants and x is the position of the particle. The acceleraion of the particle as a function of x, is given by :
01:08View Solutionएकांक द्रव्यमान का कोई कण एक विमीय गति करता है ओर इसका वेग समीकरण v(x)=bx−2n के अनुसार परिवर्तित होता है, जहाँ b तथा n स्थिरांक हैं तथा x कण कि स्थिति है। इस कण के त्वरण को x के फलन के रूप में निरूपित किया जा सकता है :
03:32View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
03:04View SolutionA particle of unit mass undergoes one-dimensional motion such that its velocity varies according to v(x)=βx−2n where β and n are constants and x is the position of the particle. The acceleration of the particle as a function of x, is given by
05:22View SolutionA particle of unit mass undergoes one-dimensional motion such that its velocity varies according to
v(x)=βx−2n
where β and n are constant and x is the position of the particle. The acceleration of the particle as a function of x is given by.02:49View Solutionएकांक द्रव्यमान का कोई कण एक विमीय गति करता है ओर इसका वेग समीकरण v(x)=bx−2n के अनुसार परिवर्तित होता है, जहाँ b तथा n स्थिरांक हैं तथा x कण कि स्थिति है। इस कण के त्वरण को x के फलन के रूप में निरूपित किया जा सकता है :
03:04View Solutionएक कण इस प्रकार से एक-विमीय गति करता है कि इसका वेग v(x)=βx−2n के अनुसार परिवर्तित होता है, जहां β और n नियतांक हैं और x कण की स्थिति है। x के फलन के रूप में कण का त्वरण किसके द्वारा दिया जाता है?
03:27View Solution

