A particle of unit mass undergoes one-dimensional motion such that its velocity varies according to
where and are constant and is the position of the particle. The acceleration of the particle as a function of is given by.
The correct Answer is:B
Step by step video & image solution for A particle of unit mass undergoes one-dimensional motion such that its velocity varies according to v(x) = beta x^(-2 n) where beta and n are constant and x is the position of the particle. The acceleration of the particle as a function of x is given by. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The acceleration of the particle is
View SolutionIf v=x2−5x+4, find the acceleration of the particle when velocity of the particle is zero.
View SolutionA particle of mass m in a unidirectional potential field have potential energy U(x)=α+2βx2, where α and β are positive constants. Find its time period of oscillations.
View SolutionA particle located in a one-dimensional potential field has its potential energy function as U(x)ax4−bx2, where a and b are positive constants. The position of equilibrium x corresponds to
View SolutionA particle moves along a path y=ax2 (where a is constant) in such a way that x-component of its velocity (ux) remains constant. The acceleration of the particle is
View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=23s is
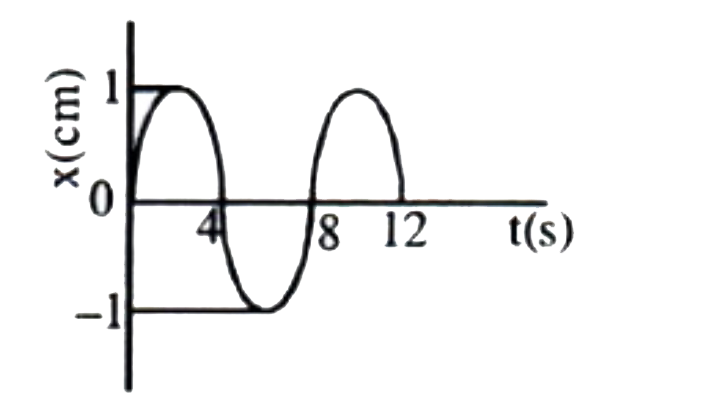
View SolutionA particle moves such that its acceleration is given by a=−β(x−2)
Here, β is a positive constnt and x the x-coordinate with respect to the origin. Time period of oscillation is
View SolutionA particle moving in the positive x-direction has initial velocity v0. The particle undergoes retardation kv2 , where vis its instantaneous velocity. The velocity of the particle as a function of time is given by:
View SolutionA particle is executing SHM and its velocity v is related to its position (x) as v2+ax2=b, where a and b are positive constant. The frequency of oscillation of particle is
View Solution
