A particle oscillating under a force →F=−k→x−b→v is a (k and b are constants)
simple harmonic oscillator
non linear oscillator
damped oscillator
forced oscillator
The correct Answer is:C
Step by step video, text & image solution for A particle oscillating under a force vecF=-kvecx-bvecv is a (k and b are constants) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONS BOOK - TARGET PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - EVALUATION TEST
14 Videos
- OSCILLATIONS BOOK - TARGET PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Critical thinking
81 Videos
- MODEL QUESTION PAPER BOOK - TARGET PUBLICATIONCHAPTER - MODEL QUESTION PAPER EXERCISE - MODEL QUESTION PAPER -II
47 Videos
- QUESTION PAPER 2019BOOK - TARGET PUBLICATIONCHAPTER - QUESTION PAPER 2019EXERCISE - MCQ
45 Videos
Similar Questions
A particle of mass 0.1kg executes SHM under a force F=−10x(N). Speed of particle at mean position is 6m/s. Find its amplitude of oscillation.
View SolutionLet →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .
View Solution
Knowledge Check
Question Stimulus :-
If a=-bx is a particle motion equation where a is acceleration, x is displacement and b is constant then oscillation time period of particle is-A2√π/bB2π/bC2π/√bD2π√bAparticle of mass m oscillating as given by U(y)=K|y|3 with force constant K has an amplitude A. The maximum velocity during the oscillation is proportional to
AABA3CA3/2DA1/2A particle of mass m oscillates inside a smooth spherical shell of radius R and starts its motion from point B. At given instant the kinetic energy of the particle is K. Then the force applied by particle on the shell at this instant is :−
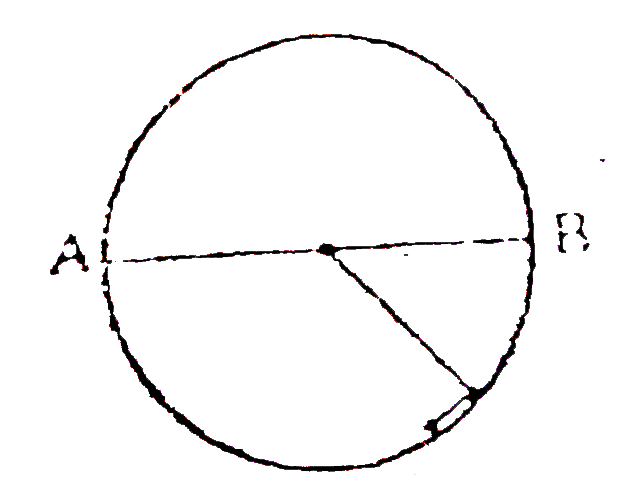 AKRB2KRC3KRDK2R
AKRB2KRC3KRDK2R
A particle is moving under constant acceleration a=kt. The motion starts from rest. The velocity and displacement as a function of time t is
View Solution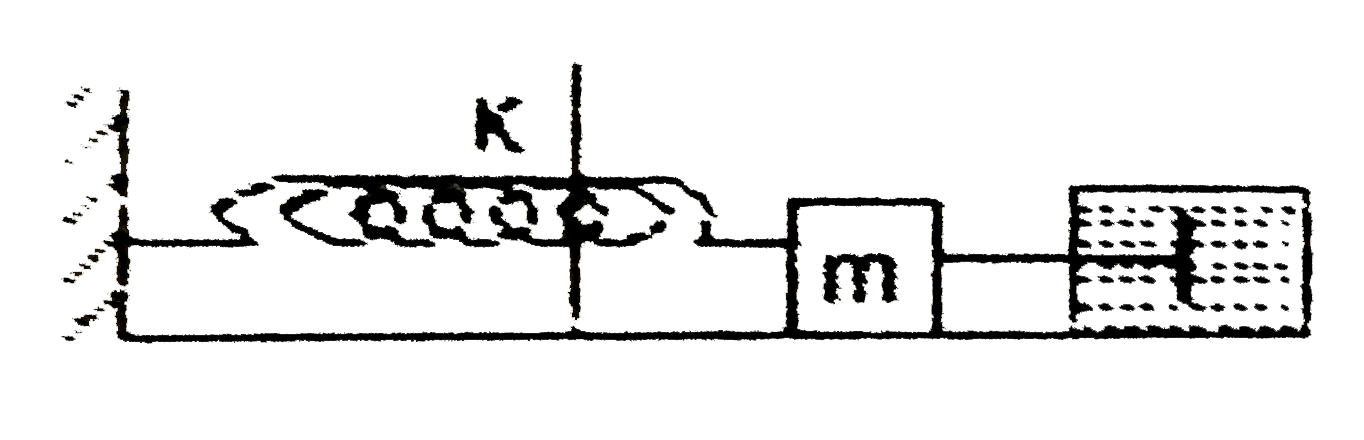
For a damped oscillator which follow the equation →F=−k→x−b→V
the mass of the block is 100 gm K=100N/M and the damping constant is 20 gm/sec. thhen find the time taken for its mechanical energy to drop to one-fourth of its initial value.
View SolutionA particle of mass m is under the influence of a force F which varies with the displacement x according to the relation F=−kx+F0 in which k and F0 are constants. The particle when disturbed will oscillate
View SolutionUnder the action of a force F=−kx3 , the motion of a particle is (k=a positive constant)
View SolutionA particle oscillation is given by (f0)=kpl2 with for constant k and an amplitude A The maximum velocity during the oscillation a preperitiaonal to :
View Solution
