A particle P lying on a smooth horizontal x−y plane starts from (3ˆi+4ˆj)m with velocity (2ˆi)m/s. Another particle Q is projected (horizontally from origin with velocity (xˆi+yˆj) so that is strikes P after 2s. Then
x=2.0
x=3.5
y=2.0
y=3.5
The correct Answer is:B, C
Step by step video, text & image solution for A particle P lying on a smooth horizontal x-y plane starts from (3hati+4hatj)m with velocity (2hati)m//s. Another particle Q is projected (horizontally from origin with velocity (xhati+yhatj) so that is strikes P after 2s. Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - MATCH THE COLUMN
10 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A particle P is at the origin starts with velocity u=(2ˆi−4ˆj)m/s with constant acceleration (3ˆi+5ˆj)m/s2. After travelling for 2s its distance from the origin is
View SolutionAcceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View Solution
Knowledge Check
A particle is projected from ground with velocity 3ˆi+4ˆi m/s. Find range of the projectile :-
A1.2mB3.6mC2.4mD10mA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
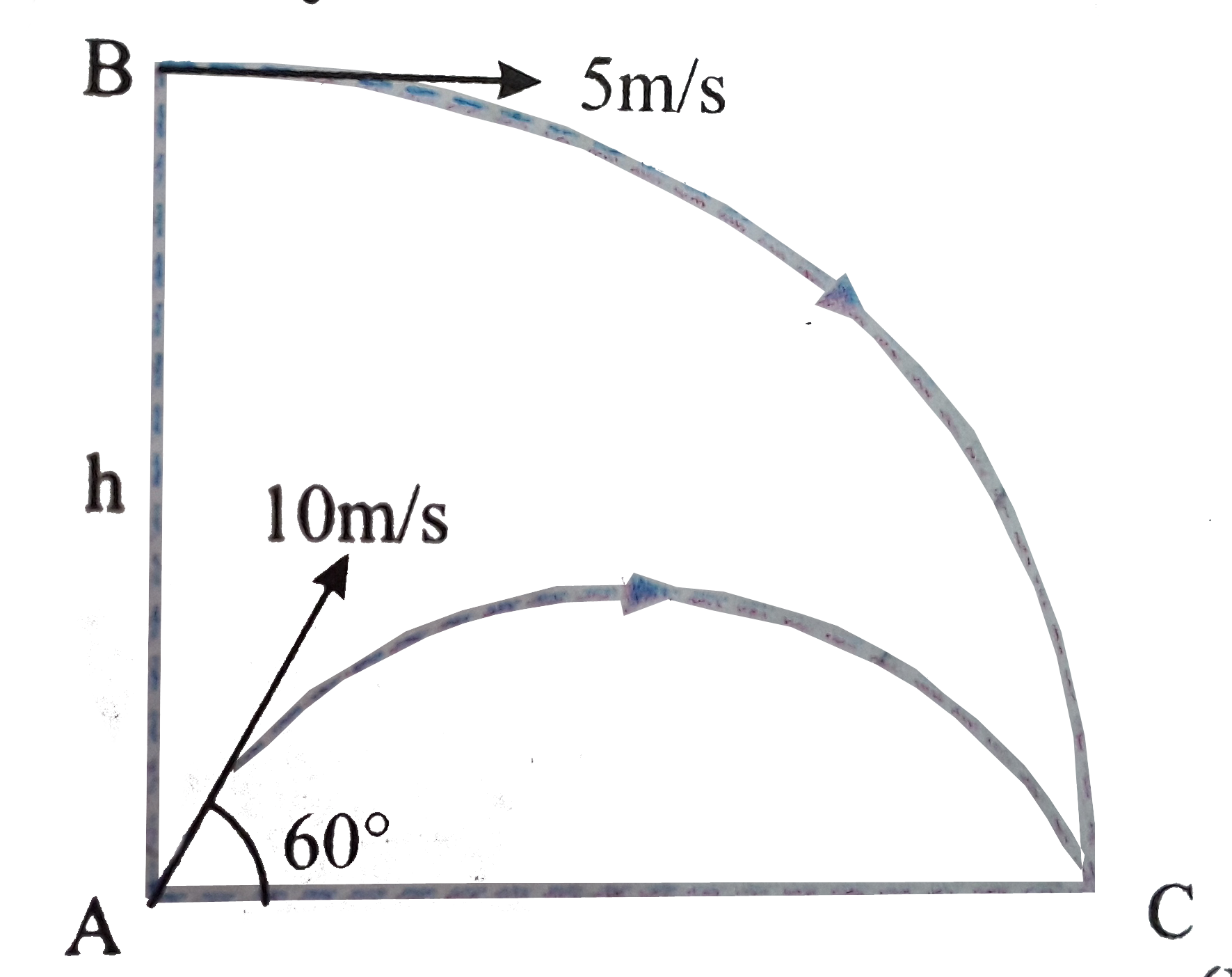 A10mB15mC20mD30m
A10mB15mC20mD30mA particle is projected with velocity u at an angle α from a point P on a horizontal plane strikes the plane at Q. The average velocity of the particle for its journey from P to Q is-
Ausinα2BucosαCu2Dusinα4
A particle is projected from ground with velocity 50m/s at 37∘ from horizontal. Find velocity and displacement after 2 s. sin37∘=35.
View SolutionA particle of mass m moving with a velocity (3ˆi+2ˆj)ms−1 collides with another body of mass M and finally moves with velocity (−2ˆi+ˆj)ms−1. Then during the collision
View SolutionVelocity of a particle changes from (3ˆi+4ˆj)m/s to (6ˆi+5ˆj)m/s 2s. Find magnitude and direction of average acceleration.
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
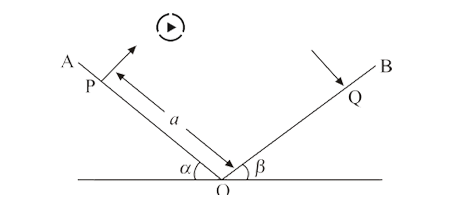
The path of the particle from P to Q is
View SolutionA particle moving with velocity (2ˆi−3ˆj) m/s collides with a surface at rest in xz–plane as shown in figure and moves with velocity (2ˆi+2ˆj) m/s after collision. Then coefficient of restitution is :
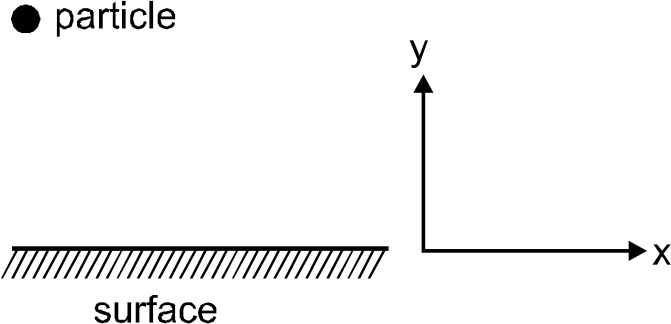
View Solution
