A particle starts from a pointn A and travels along the solid curve shown in figure. Find approximately the position B of the particle such that the average velocity between the positions A and B has the same direction as the instantaneous velocity at B.

The correct Answer is:C
AT position B instasntaneous velocity has direction along −−→BC For average velocity between A and B Vav=displacementtime<br>=⎛⎝−−→ABt⎞⎠<br> We can see that vec(AB) is along (BC) i.e. they are in same direction. The point is B (5m, 3,).
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective 2
10 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
Similar Questions
A particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View SolutionA particle starts from rest at the origin and moves along the positive x direction. Its acceleration a versus position x graph is shown in the figure. The velocity of the particle at x = 6 m is?
View Solution
Knowledge Check
The acceleration of a particle starting from rest and travelling along a straight line is shown in figure. The maximum speed of the particle is
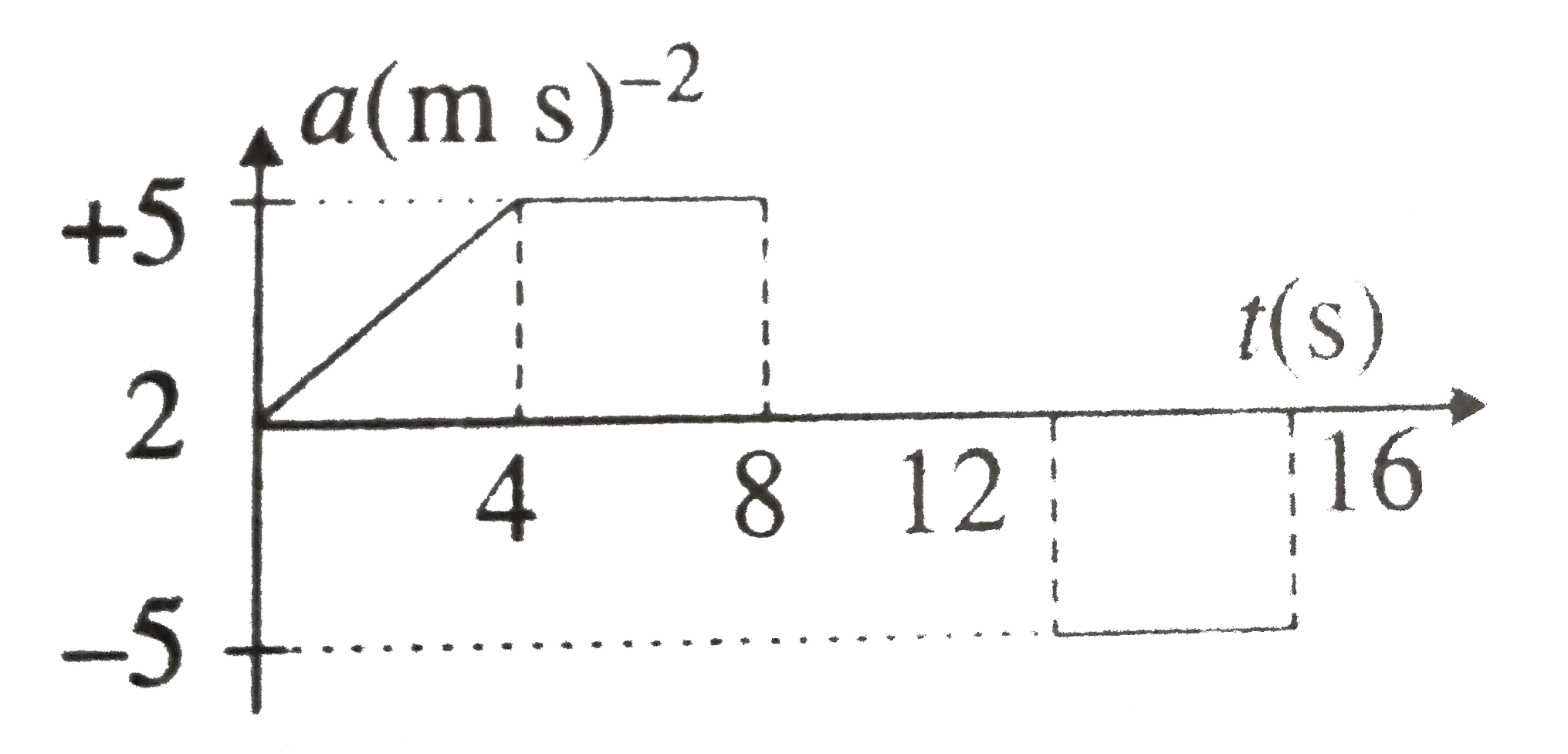 A20ms−1B30ms−1C40ms−1D60ms−1
A20ms−1B30ms−1C40ms−1D60ms−1Position - time graph for a particle is shown in figure. Starting from t = 0, at what time t, the average velocity is zer?
 A1 sB3 sC6 sD7 s
A1 sB3 sC6 sD7 sIf a particle starts from a along the curved circular path shown in figure with tangential acceleration 'a'. Then acceleration at B in magnitude is :
 A2a√1+π2Ba√1+π2Ca√π2−1Daπ√1+π2
A2a√1+π2Ba√1+π2Ca√π2−1Daπ√1+π2
From the velocity time plot shown in figure find the distance travelled by the particle dureing the first 40 seconds. Also find the average velocity during this period.

View SolutionThe position time graph of a particle is shown below. The point where velocity is negative and acceleration is positive is х a b
View SolutionIn one second, a particle goes from point A to point B moving in a semicircle (Fig). Find the magnitude of the average velocity.
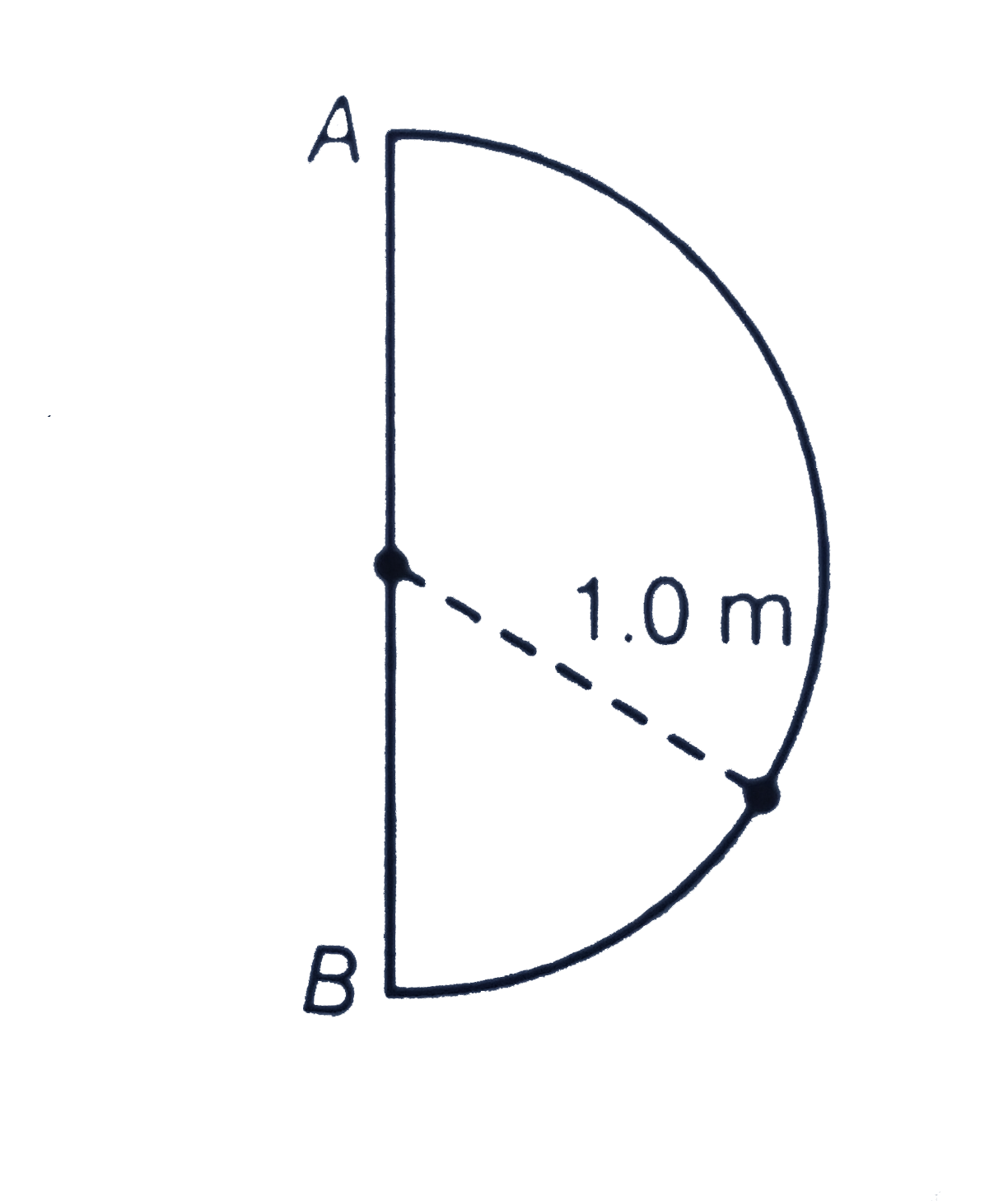
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionIf a particle of mass m start from along curved circular path shown in figure with constant tangential acceleration a, then net force at B on the particle has the magnitude :

View Solution
