A particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
2m/s
3m/s
4m/s
6m/s
The correct Answer is:B
The area of a-t graph gives change in velocity.
Area of a-t graph between t=0 and t=3s is
(3×2)+(−3×1)=3
vt=3−vt=0=area of a-t graph
vt=3−0=3⇒vt=3=3m/s
Topper's Solved these Questions
Similar Questions
A particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
View Solution
Knowledge Check
- Question 1 - Select One
A particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
A5m/s2B6m/s2C10m/s2D15m/s2 - Question 2 - Select One
A particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
A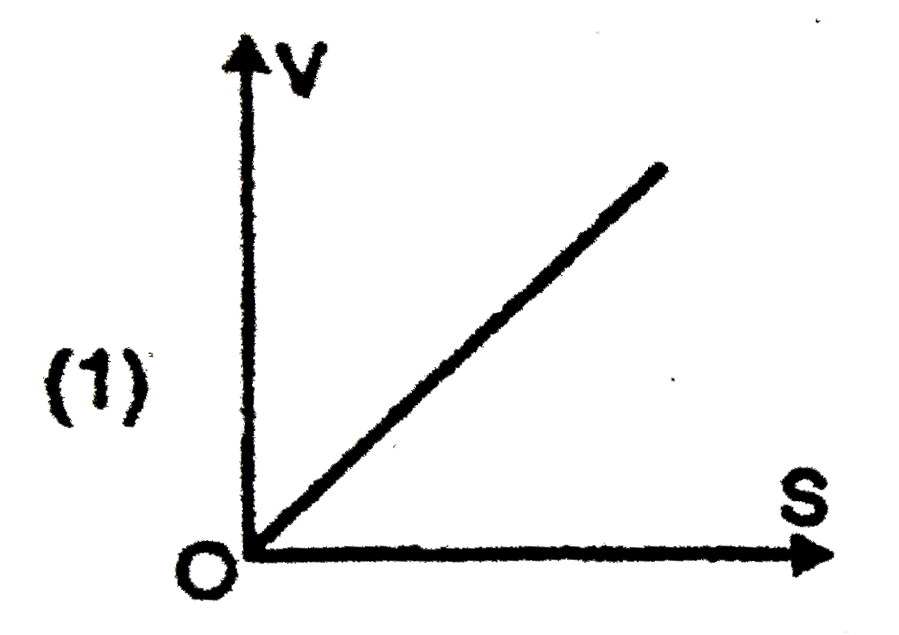
B
C
D
A particle starts from rest at t=0 and moves along a straight line with a variable acceleration given by a (t)=(3t+1)ms−2 ,where t],[ is in seconds.The velocity of the particle at t=4s is
View SolutionThe acceleration after t seconds of a particle which starts from rest and moves in a straight line is (8−t5)cms2. Find the velocity of the particle when the acceleration is zero.
View SolutionA particle starts moving from rest on a straight line. Its acceleration a verses time t is shown in the figure. The speed of the particle is maximum at the instant
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q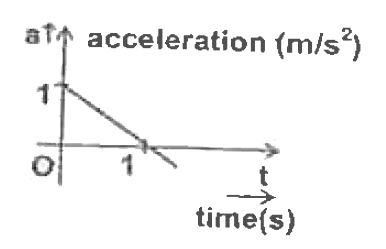
View SolutionA particle, starting from rest, moves in a straight line with constant acceleration a0 for a time interval t0.Then is accelerates at a constant rate 2a0 for time interval 2t0 .The distance travelled by the particle in time 3t0 from the starts is S . Then Sa0t20=
View Solution