A particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
2m/s
4m/s
zero
12m/s
To find the velocity of a particle at t=4 seconds, given the acceleration a=2+|t−2|m/s2, we will follow these steps:
Step 1: Define the acceleration function
The acceleration function can be expressed as:
a(t)=2+|t−2|
To handle the absolute value, we need to consider two cases based on the value of t.
Step 2: Determine the cases for |t−2|
1. Case 1: When t<2:
|t−2|=2−t⇒a(t)=2+(2−t)=4−t
2. Case 2: When t≥2:
|t−2|=t−2⇒a(t)=2+(t−2)=t
Step 3: Find the velocity from t=0 to t=2
For 0≤t<2, we have:
a(t)=4−t
Using the relation a=dvdt:
dvdt=4−t
Integrating both sides from t=0 to t=2:
∫v20dv=∫20(4−t)dt
Calculating the right side:
v2−v0=(4t−t22)20=(4(2)−(2)22)−0=8−2=6
Since the particle starts from rest, v0=0:
v2=6m/s
Step 4: Find the velocity from t=2 to t=4
For 2≤t<4, we have:
a(t)=t
Again using a=dvdt:
dvdt=t
Integrating from t=2 to t=4:
∫v4v2dv=∫42tdt
Calculating the right side:
v4−v2=(t22)42=((4)22−(2)22)=(162−42)=8−2=6
Thus,
v4=v2+6=6+6=12m/s
Final Answer
The velocity of the particle at t=4 seconds is:
12m/s
The acceleration function can be expressed as:
a(t)=2+|t−2|
To handle the absolute value, we need to consider two cases based on the value of t.
1. Case 1: When t<2:
|t−2|=2−t⇒a(t)=2+(2−t)=4−t
2. Case 2: When t≥2:
|t−2|=t−2⇒a(t)=2+(t−2)=t
For 0≤t<2, we have:
a(t)=4−t
Using the relation a=dvdt:
dvdt=4−t
Integrating both sides from t=0 to t=2:
∫v20dv=∫20(4−t)dt
Calculating the right side:
v2−v0=(4t−t22)20=(4(2)−(2)22)−0=8−2=6
Since the particle starts from rest, v0=0:
v2=6m/s
For 2≤t<4, we have:
a(t)=t
Again using a=dvdt:
dvdt=t
Integrating from t=2 to t=4:
∫v4v2dv=∫42tdt
Calculating the right side:
v4−v2=(t22)42=((4)22−(2)22)=(162−42)=8−2=6
Thus,
v4=v2+6=6+6=12m/s
The velocity of the particle at t=4 seconds is:
12m/s
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A particle starts from rest and moves with a constant acceleration of 4m/s2 for 10s, then it moves under constant seceleration and stops in 20s. Find (a) the maximum velocity attained by the particle (b) the total distance traveled and (c ) the distance/distances from the origin, when the particle is moving at half the maximum velocity.
View SolutionA particle starts from rest with acceleration 2m/s2. The acceleratioin of the particle of the particle descreases down to zero uniformly during time -interval of 4s. The velocity of particle after 2s is
View Solution
Knowledge Check
A particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 A5m/s2B6m/s2C10m/s2D15m/s2
A5m/s2B6m/s2C10m/s2D15m/s2A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A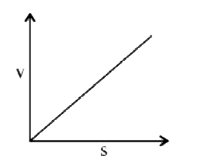 B
B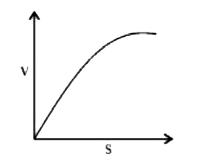 C
C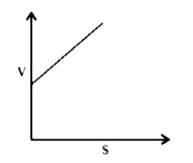 D
D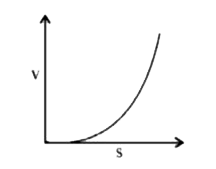
Starting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
A15 m/sB25 m/sC5 m/sDNone of these
The acceleration after t seconds of a particle which starts from rest and moves in a straight line is (8−t5)cms2. Find the velocity of the particle when the acceleration is zero.
View SolutionA particle is moving with initial velocity 1m/s and acceleration a=(4t+3)ms2. Find velocity of particle at t=2sec.
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View SolutionThe acceleration of a particle which starts from rest varies with time according to relation a=2t+3. The velocity of the particle at time t would be
View SolutionStarting from rest, acceleration of a particle is a=2t(t−1). The velocity of the particle at t=5s is
View Solution
