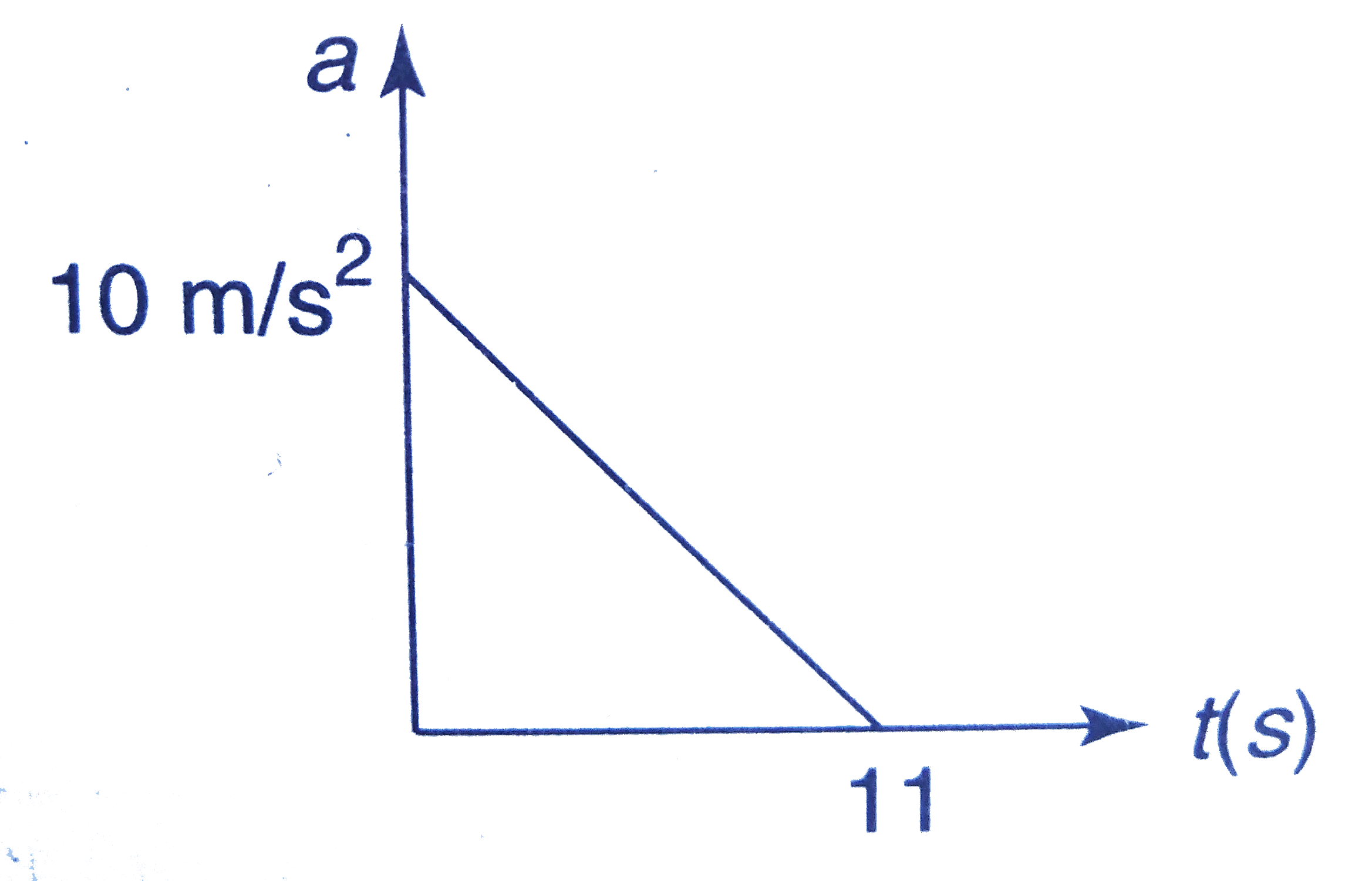
A particle starts from rest. Its acceleration (a) versus time (t) graph is as shown in the figure. The maximum speed of the particle will be 
110 m/s
55m/s
550m/s
660 m/s
The correct Answer is:B
Step by step video solution for A particle starts from rest. Its acceleration (a) versus time (t) graph is as shown in the figure. The maximum speed of the particle will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
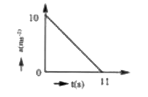
A particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.
View SolutionA particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.

View SolutionA particle starts moving from rest on a straight line. Its acceleration a verses time t is shown in the figure. The speed of the particle is maximum at the instant

View SolutionA particle starts from rest. Its acceleration at time t=0 is 5m/s2 which varies with time as shown in the figure. The maximum speed of the particle will be
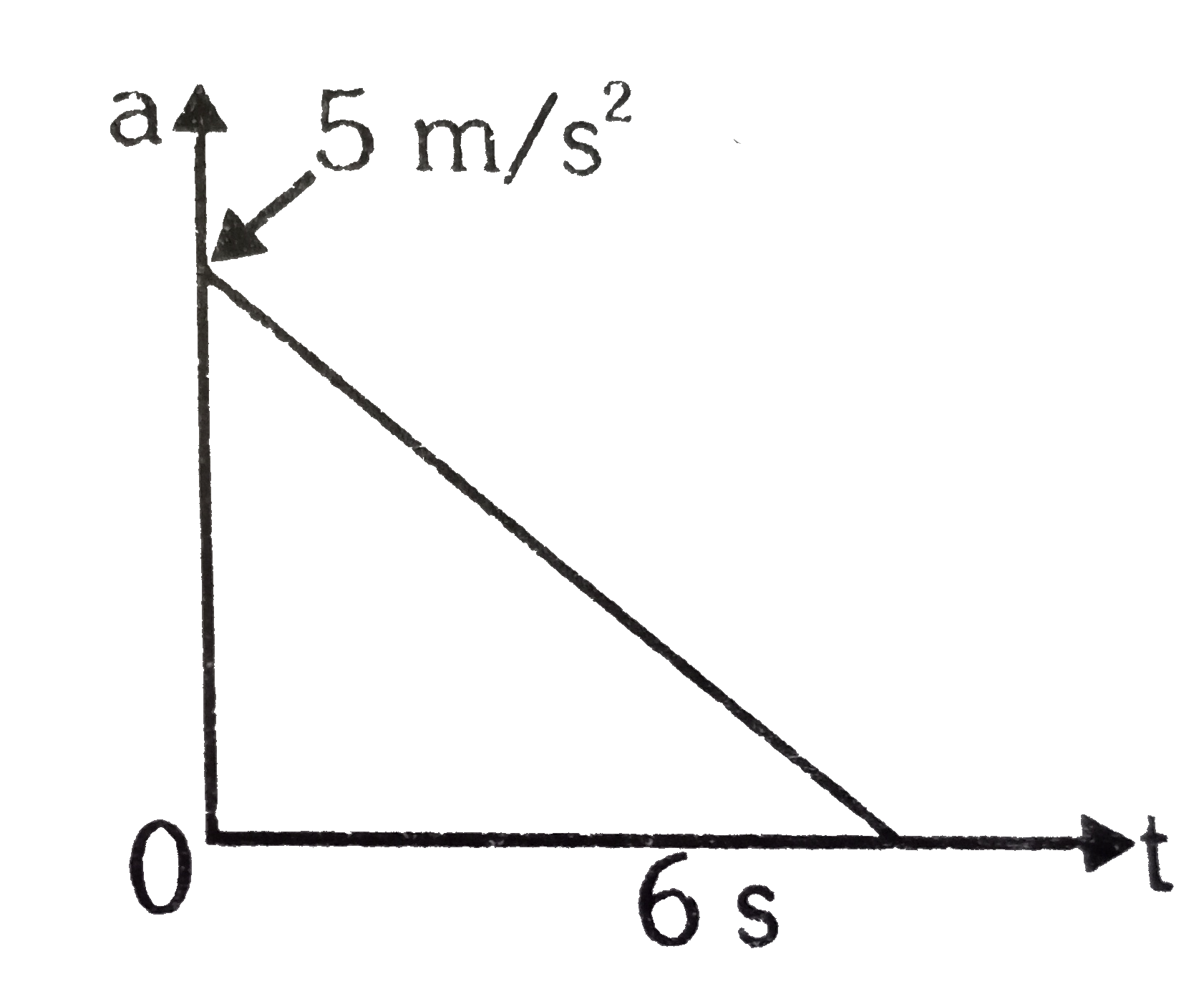
View SolutionThe acceleration of a particle starting from rest and travelling along a straight line is shown in figure. The maximum speed of the particle is
View SolutionThe a -t graph is shown in the figure. The maximum velocity attained by the body from rest will be
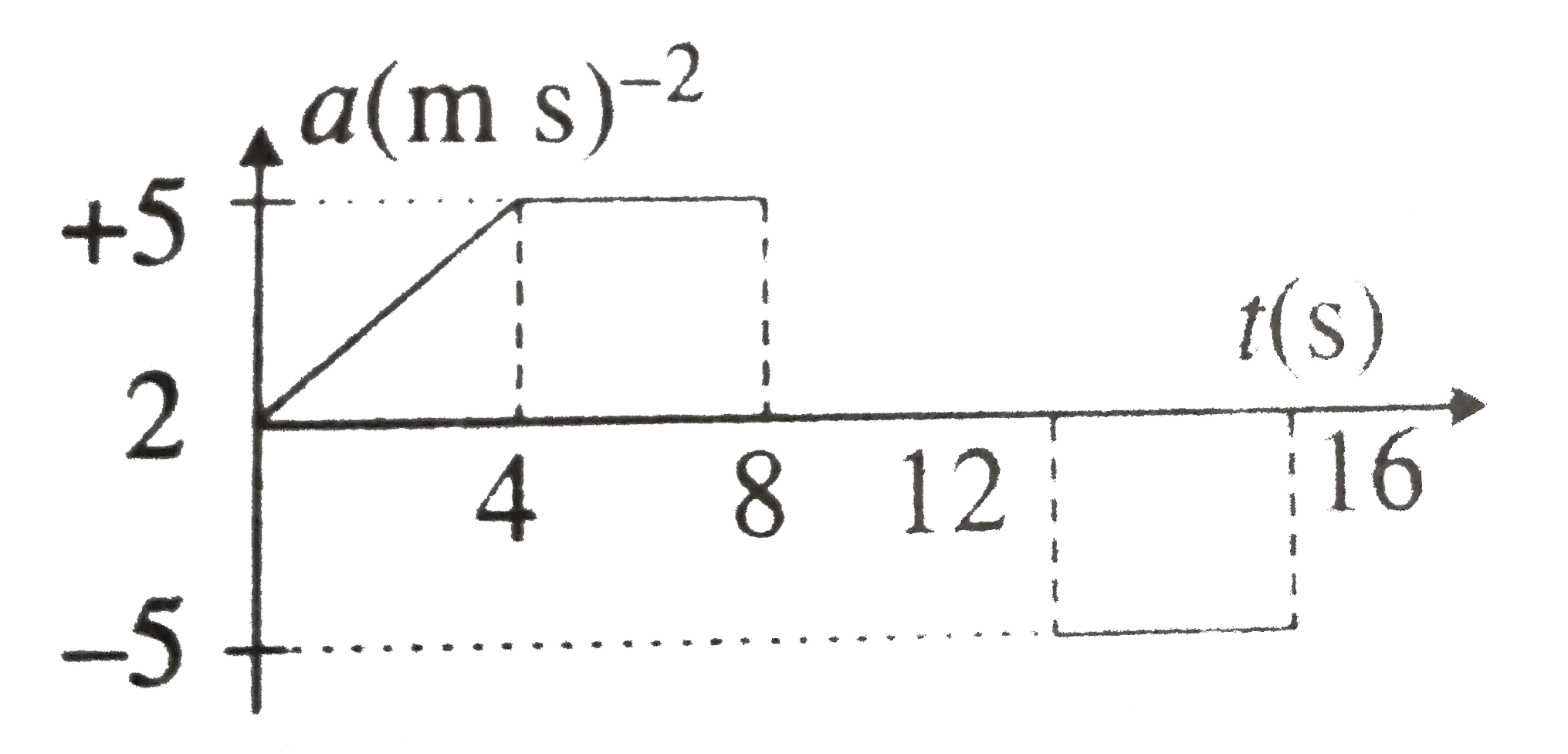
View SolutionA particle starts from rest. Its acceleration is varying with time as shown in the figure. When the particle comes to rest, its distance from its starting point is

View SolutionA particle starts from rest at time t=0 and moves on a straight line with acceleration as plotted in fig. The speed of the particle will be maximum after time.

View SolutionThe acceleration versus time graph of a particle is shown in. The respective v−t graph of the particle is .
 .
.
View SolutionA Body intially at rest, starts moving along x−axis in such a way so that its acceleration vs displacement plot is as shown in figure. The maximum velocity of particle is :−

View Solution
