A particle starts from the origin, goes along X-axis to the point (30m, 0) and then returns along the same line to the point (-30m,0). The displacement and distance of the particle during the trip are
0, 60m
60m,30m
90m, -30m
−30m,90m
The correct Answer is:D
To solve the problem, we need to determine both the displacement and the distance traveled by the particle during its trip. Let's break it down step by step.
Step 1: Understand the motion of the particle
The particle starts at the origin (0, 0), moves to the point (30 m, 0), and then returns to the point (-30 m, 0).
Step 2: Calculate the displacement
Displacement is defined as the shortest straight-line distance from the initial position to the final position, along with the direction.
- Initial Position: (0, 0)
- Final Position: (-30, 0)
Displacement can be calculated using the formula:
Displacement=Final Position−Initial Position
Substituting the values:
Displacement=−30m−0m=−30m
Step 3: Calculate the distance
Distance is the total length of the path traveled, regardless of direction.
1. The particle first travels from the origin to (30 m, 0), which is a distance of 30 m.
2. Then, it returns from (30 m, 0) to (-30 m, 0). This return journey is another 60 m (30 m to return back to the origin and then another 30 m to reach (-30 m, 0)).
Total distance traveled can be calculated as:
Total Distance=Distance to (30 m, 0)+Distance to (-30 m, 0)
Total Distance=30m+60m=90m
Step 4: Summarize the results
- Displacement: -30 m
- Total Distance: 90 m
Final Answer
- Displacement: -30 m
- Distance: 90 m
The particle starts at the origin (0, 0), moves to the point (30 m, 0), and then returns to the point (-30 m, 0).
Displacement is defined as the shortest straight-line distance from the initial position to the final position, along with the direction.
- Final Position: (-30, 0)
Displacement=Final Position−Initial Position
Displacement=−30m−0m=−30m
Distance is the total length of the path traveled, regardless of direction.
2. Then, it returns from (30 m, 0) to (-30 m, 0). This return journey is another 60 m (30 m to return back to the origin and then another 30 m to reach (-30 m, 0)).
Total Distance=Distance to (30 m, 0)+Distance to (-30 m, 0)
Total Distance=30m+60m=90m
- Displacement: -30 m
- Total Distance: 90 m
- Displacement: -30 m
- Distance: 90 m
Topper's Solved these Questions
- MOTIONBOOK - MCGROW HILL PUBLICATIONCHAPTER - MOTIONEXERCISE - HIGHER ORDER THINKING QUESTIONS
48 Videos
- MISCELLANEOUS QUESTIONSBOOK - MCGROW HILL PUBLICATIONCHAPTER - MISCELLANEOUS QUESTIONSEXERCISE - PART-B
99 Videos
- REFLECTION OF LIGHT BOOK - MCGROW HILL PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - HIGHER ORDER THINKING QUESTIONS
10 Videos
Similar Questions
A particle starts from the origin, goes along the X-axis to the pont (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
View SolutionA particle starts from the origin,goes along the "X" - axis to the point(20m,0) and then returns along the same line to the point (-20m,0 then the displacement of the particle during the trip in negative direction is....(in m )
View Solution
Knowledge Check
A particle starts from the origin, goes along x-axis to the point (10 m, 0) and then returns along. The same line to the point (-10 m, 0). The distance and displacement of the particle during the trip are
A20 m, 0B30 m, 10 mC30 m, - 10 mD20 m, 10 mA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
A−2Ka2B2Ka2C−Ka2DKa2
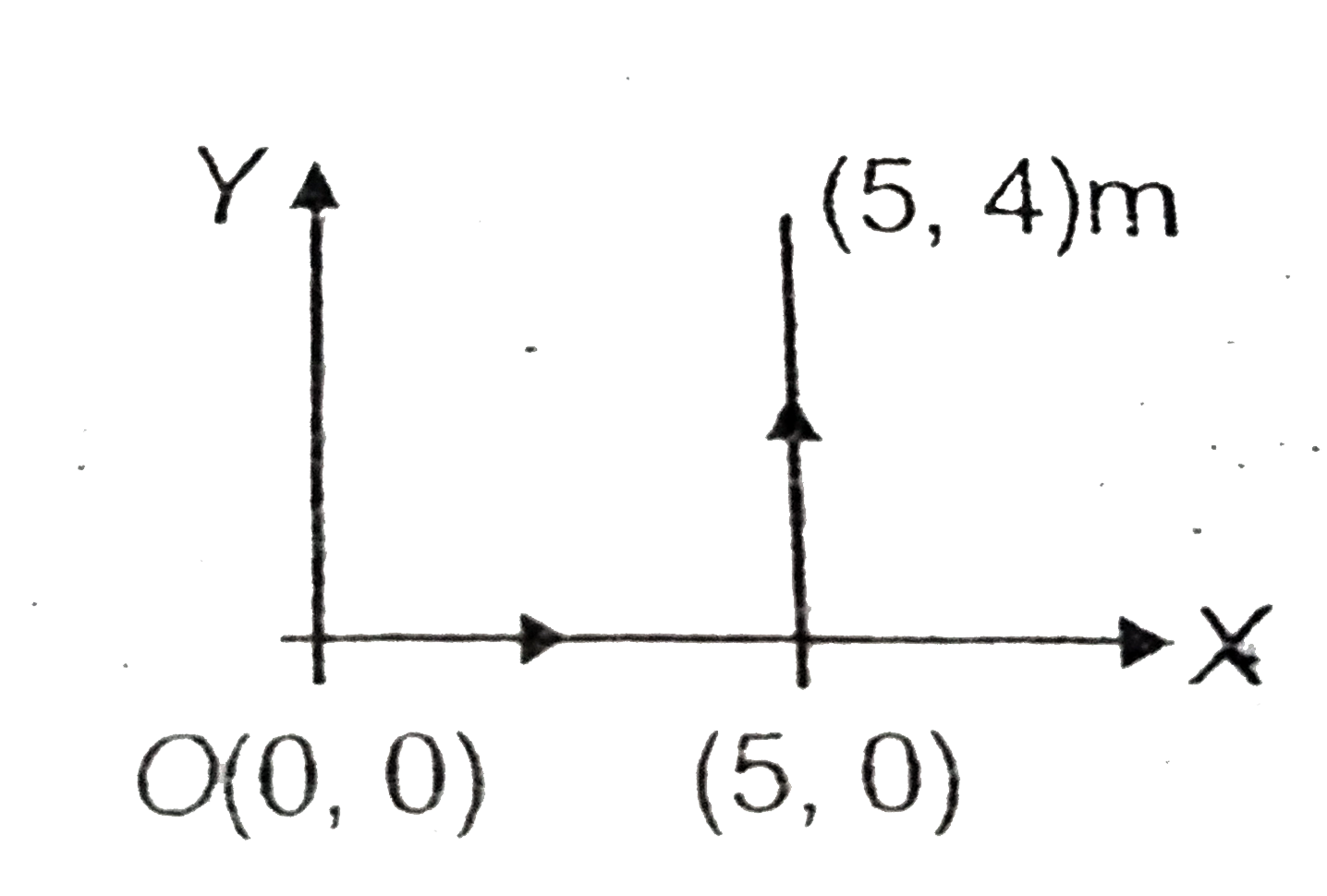
A force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
View SolutionA force →F(yˆl+xˆJ), where K is a positive constant, acts on a particle moving in the XY-Plane. Starting from the origin, the particle is taken along the positive X-axis to a point (a,0) and then parallel to the y-axis to the point (a,a). Calculate the total work done by the force on the particle.
View SolutionA particle is moving along the x-axis such that s=6t−t2, where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5s.
View SolutionA force →F=(3→i+4→j)N, acts on a particle moving in x-y plane. Starting from origin, the particle first goes along x-axis to thepoint (4,0)m and then parallel to the y -axis to the point(4, 3)m. The total work done by the force on the particle is
(##NAR_NEET_PHY_XI_P2_C06_E09_014_Q01.png" width="80%">
View SolutionA force F=−K(yˆI+xˆj)(whereKisaposiveconstant)actsonapartic≤mov∈g∈thexypla≠.Start∈gformtheorig∈al,theparticalistakenalong∈thepositivexaξs→thep∮(x,0)andthenpartical→theyaξsthep∮(x,0).The→talworkdo≠bytheforceF on the particls is
View Solution
