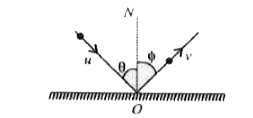
A particle strikes a horizontal frictionless floor with a speed u at an angle $θ$ with the vertical, and rebounds with a speed v at an angle $ϕ$ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is

A

$e u$

B

$(1 - e) u$

C

$u \sqrt{e^{2} {sin}^{2} θ + {cos}^{2} θ}$

D

$u \sqrt{{sin}^{2} θ + e^{2} {cos}^{2} θ}$

Text Solution

Verified by Experts

The correct Answer is:D

As the floor is frictionless and there is no horizontal force, therefire, momentum must be conserved in the horizontal direction.
i.e., $m u sin θ = m v sin ϕ or u sin θ = v sin ϕ . . (i)$
And in vertical direction, $\frac{v cos ϕ}{u cos θ} = 3$
or $v cos ϕ = e u cos θ ... ... . . (i i)$
Squaring and adding (i) and (ii), we get
$v^{2} ({sin}^{2} ϕ + {cos}^{2} ϕ) = u^{2} {sin}^{2} ϕ + e^{2} u^{2} {cos}^{2} θ$
or $v = u \sqrt{{sin}^{2} ϕ + e^{2} {cos}^{2} θ}$ .

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

A particle strikes a horizontal frictionless floor with a speed u, at an angle $θ$ to the vertical, and rebounds with a speed $v$ , at an angle $ϕ$ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is

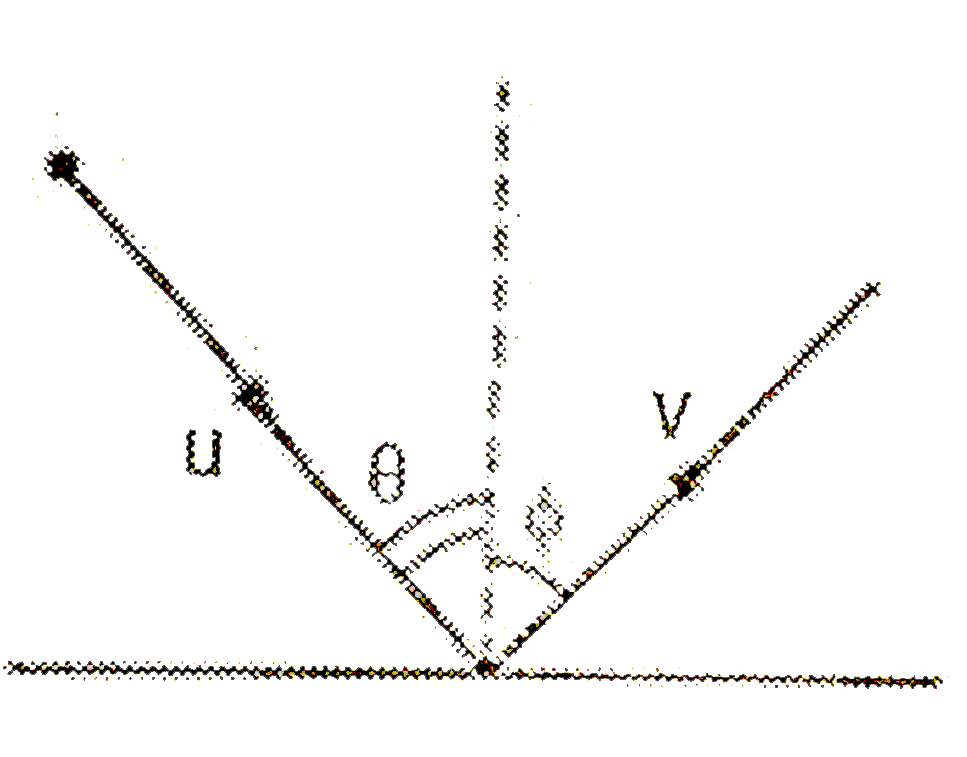Aeu
B $(1 - e) u$
C $u \sqrt{{sin}^{2} θ + e^{2} {cos}^{2} θ}$
D $u \sqrt{e^{2} {sin}^{2} θ + {cos}^{2} θ}$
A particle strikes a horizontal frictionless floor with a speed u at an angle $θ$ with the vertical, and rebounds with a speed v at an angle $ϕ$ with vertical. The coefficient of restitution between the particle and floor is e. The angle $ϕ$ is equal to

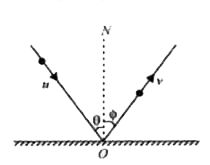A $θ$
B $(1 + e) θ$
C ${tan}^{- 1} (e tan θ)$
D ${tan}^{- 1} (\frac{1}{e} tan θ)$
A particle strikes a horizontal frictionless floor with a speed u, at an angle $θ$ with the vertical, and rebounds with a speed $υ$ , at an angle $ϕ$ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle $ϕ$ is equal to :

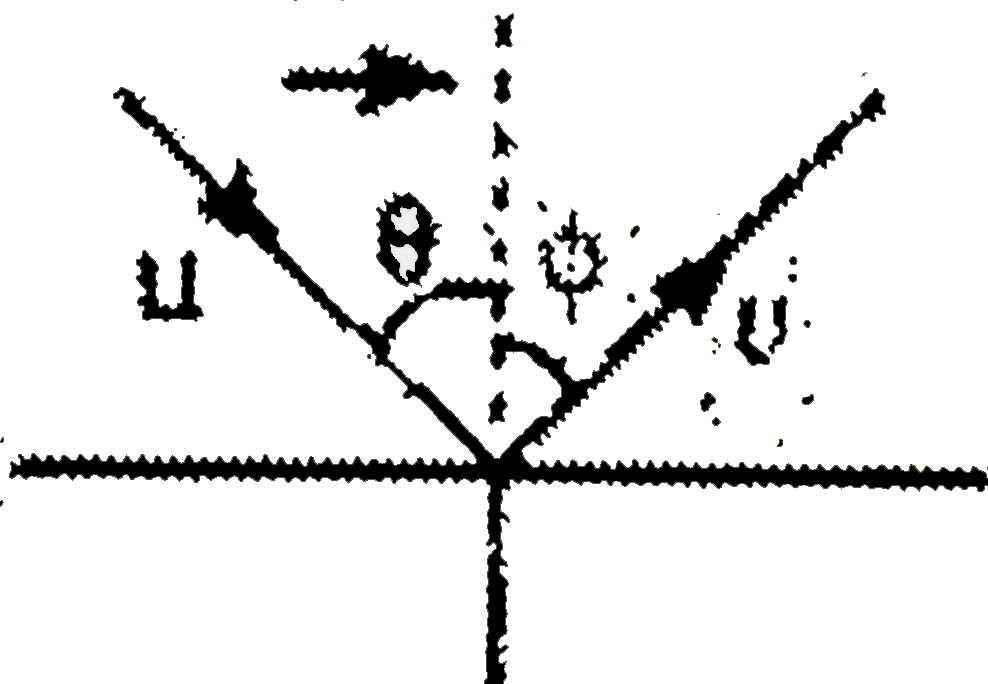A $θ$
B ${tan}^{- 1} [e tan θ]$
C ${tan}^{-!} [\frac{1}{e} tan θ]$
D $(1 + e) θ$

MTG GUIDE-WORK, ENERGY AND POWER-NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (COLLISIONS)

Home
Ask Doubt
Profile