A particle strikes a horizontal frictionless floor with a speed u at an angle $θ$ with the vertical, and rebounds with a speed v at an angle $ϕ$ with vertical. The coefficient of restitution between the particle and floor is e. The angle $ϕ$ is equal to

A

$θ$

B

$(1 + e) θ$

C

$\tan^{- 1} (e \tan θ)$

D

$\tan^{- 1} (\frac{1}{e} \tan θ)$

Text Solution

Verified by Experts

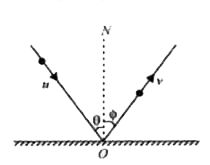
The correct Answer is:D

As the floor is frictionless and there is no horizontal force, therefore, momentum must be conserved in the horizontal direction.
i.e, $m u \sin θ = m v \sin ϕ or u \sin θ = v \sin θ \dots . (i)$
And in vertical direction, $\frac{v \cos ϕ}{u \cos θ} = e$
or $v \cos ϕ = e u \cos θ ... . . (i i)$
Divide (i) by (ii), we get
$\tan ϕ = \frac{1}{e} \tan ϕ or ϕ = \tan^{- 1} [\frac{1}{e} \tan ϕ]$ .

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

A particle strikes a horizontal frictionless floor with a speed u at an angle $θ$ with the vertical, and rebounds with a speed v at an angle $ϕ$ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is

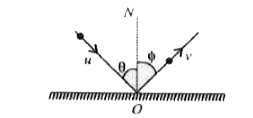A $e u$
B $(1 - e) u$
C $u \sqrt{e^{2} {sin}^{2} θ + {cos}^{2} θ}$
D $u \sqrt{{sin}^{2} θ + e^{2} {cos}^{2} θ}$
A particle strikes a horizontal frictionless floor with a speed u, at an angle $θ$ with the vertical, and rebounds with a speed $υ$ , at an angle $ϕ$ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle $ϕ$ is equal to :

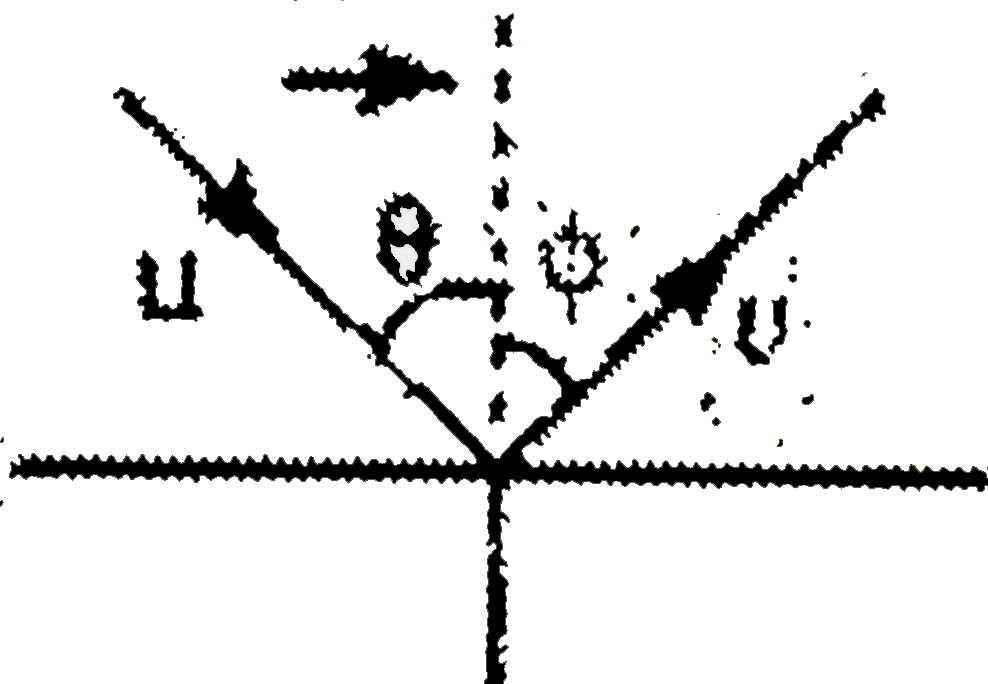A $θ$
B ${tan}^{- 1} [e tan θ]$
C ${tan}^{-!} [\frac{1}{e} tan θ]$
D $(1 + e) θ$
A particle strikes a horizontal frictionless floor with a speed u, at an angle $θ$ to the vertical, and rebounds with a speed $v$ , at an angle $ϕ$ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is

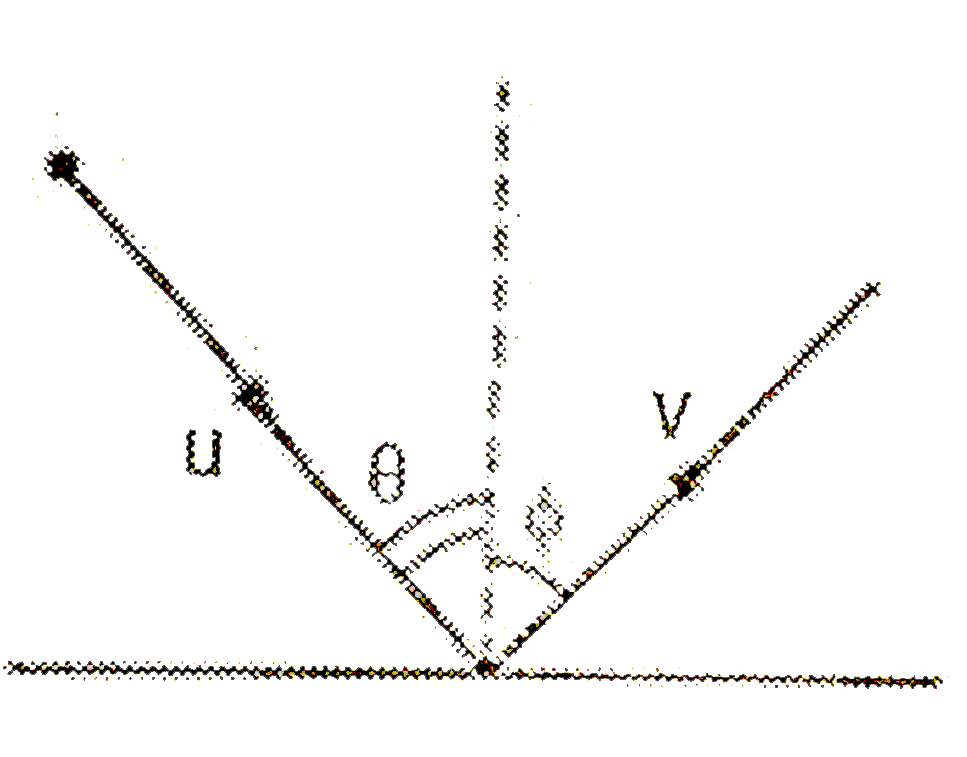Aeu
B $(1 - e) u$
C $u \sqrt{{sin}^{2} θ + e^{2} {cos}^{2} θ}$
D $u \sqrt{e^{2} {sin}^{2} θ + {cos}^{2} θ}$

MTG GUIDE-WORK, ENERGY AND POWER-NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (COLLISIONS)

Home
Ask Doubt
Profile