A particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity √7gl/2. The string will slack after swinging through an angle equal to
30∘
90∘
120∘
150∘
The correct Answer is:C
h=l+lsinθ=l(1+sinθ)
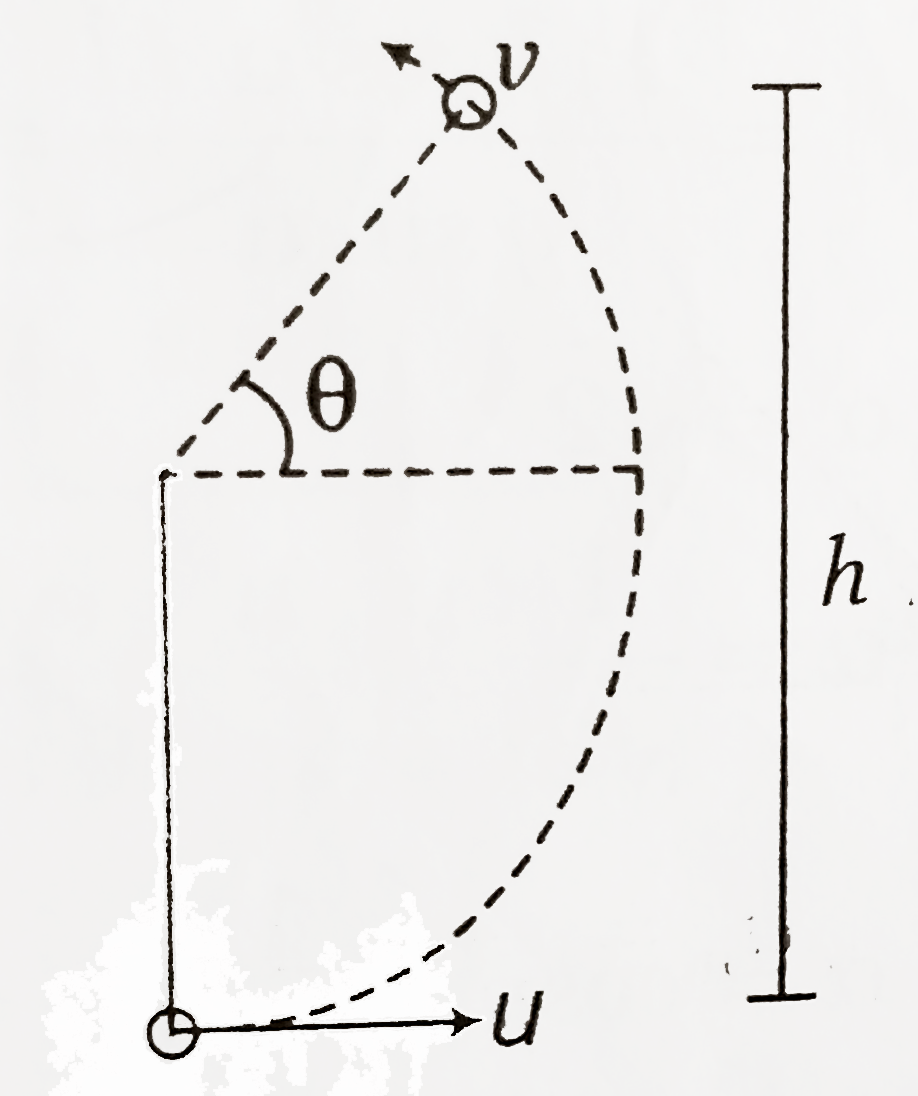
v2=u2−2gh=u2−2gl(1+sinθ)
String will slack where, component of weight towards centre is just equal to centripetal force or,
mgsinθ=mv2l=ml[u2−2gl(1+sinθ)]
Substituting u2=7gl2
we get, sinθ12 or θ=30∘
∴ The desired angle is 90∘+30∘ or 120∘
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A particle is suspended from a fixed point by a string of length 5m. It is projected from the equilibrium position with such a velocity that the string slackens after the particle has reached a height 8 m above the lowest point. Find the velocity of the particle, just before the string slackens. Find also, to what height the particle can rise further Take g=10m/s2
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View Solution
Knowledge Check
A particle suspended from a fixed point, by a light inextensible thread of length L is projected horizontally from its lowest position with velocity 7gL . The thread will slack after swinging through an angle , such that equal
A30∘B135∘C120∘D150∘A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
A√31g,cos−1(3/2)B√1g3,cos−1(2/3)C√3g3,cos−1(2/3)D√gl3,cos−1(2/3)Mass of the bob of a simple pendulum of length L is m. If the bob is projected horizontally from its mean position with velocity √4gL, then the tension in the string becomes zero after a vertical displacement of
AL/3B3L/4C4L/3D5L/3
Two particles A and B of equal masses lie close together on a horizontal table and are connected by a light inextensible string of length l. A is projected vertically upwards with a velocity √10gl. Find the velocity with which it reaches the table again.
View SolutionA bob of mass m suspended by a light inextensible string of length 'l' from a fixed point. The bob is given a speed of √6gl. Find the tension in the string when string deflects through an angle 120∘ from the vertical.
View SolutionA heavy particle is suspended by a light thread, the other end of the thread being fixed to a point O. The particle is projected from its lower position in the horizontal direction in the vertical plane through O, with such a velocity that it leaves the circular path after an angular displacement θ Show that when the string again becomes taut it makes an angle 3θ−360∘ with the downward drawn vertical.
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionA heavy particle is suspended by a string of length 60 cm from a fixed point O. it is projected horizontally with speed 4.2m/s from its lowest position : (Take g=9.8m/s2)
View Solution
