A pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where m=3kg, l=0.75m, θ=37∘. At the lowest point of the circle the tension in the string is T=274N. Take g=10ms−2.
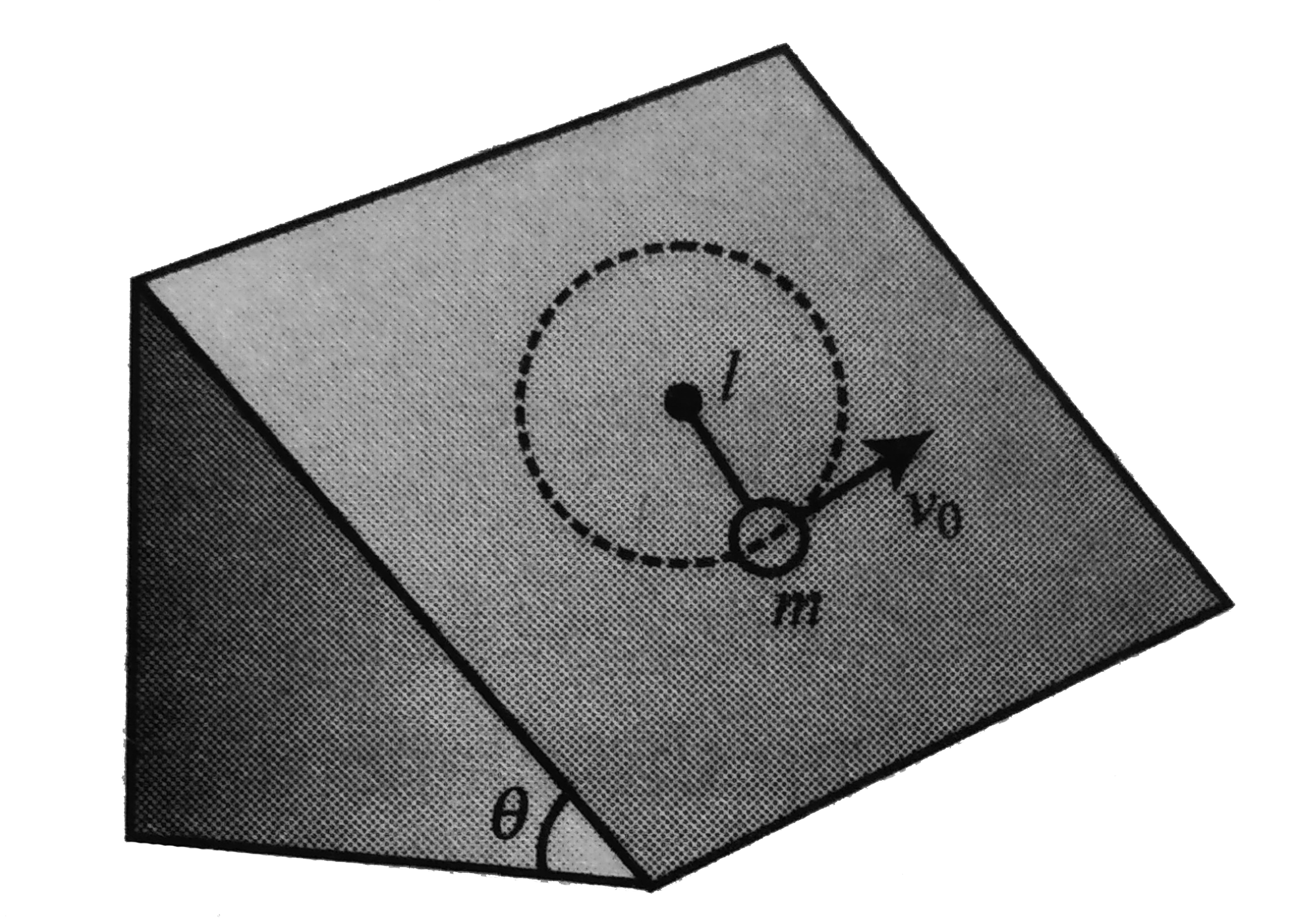
The tension in the string at the highest position is
(a) 166N
(b) 67.66N
(c) 68N
(d) 152N
The correct Answer is:A
TH+mgsin37∘=mv2Hl⇒TH=166N
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer14videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )19videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where m=3kg, l=0.75m, θ=37∘. At the lowest point of the circle the tension in the string is T=274N. Take g=10ms−2.
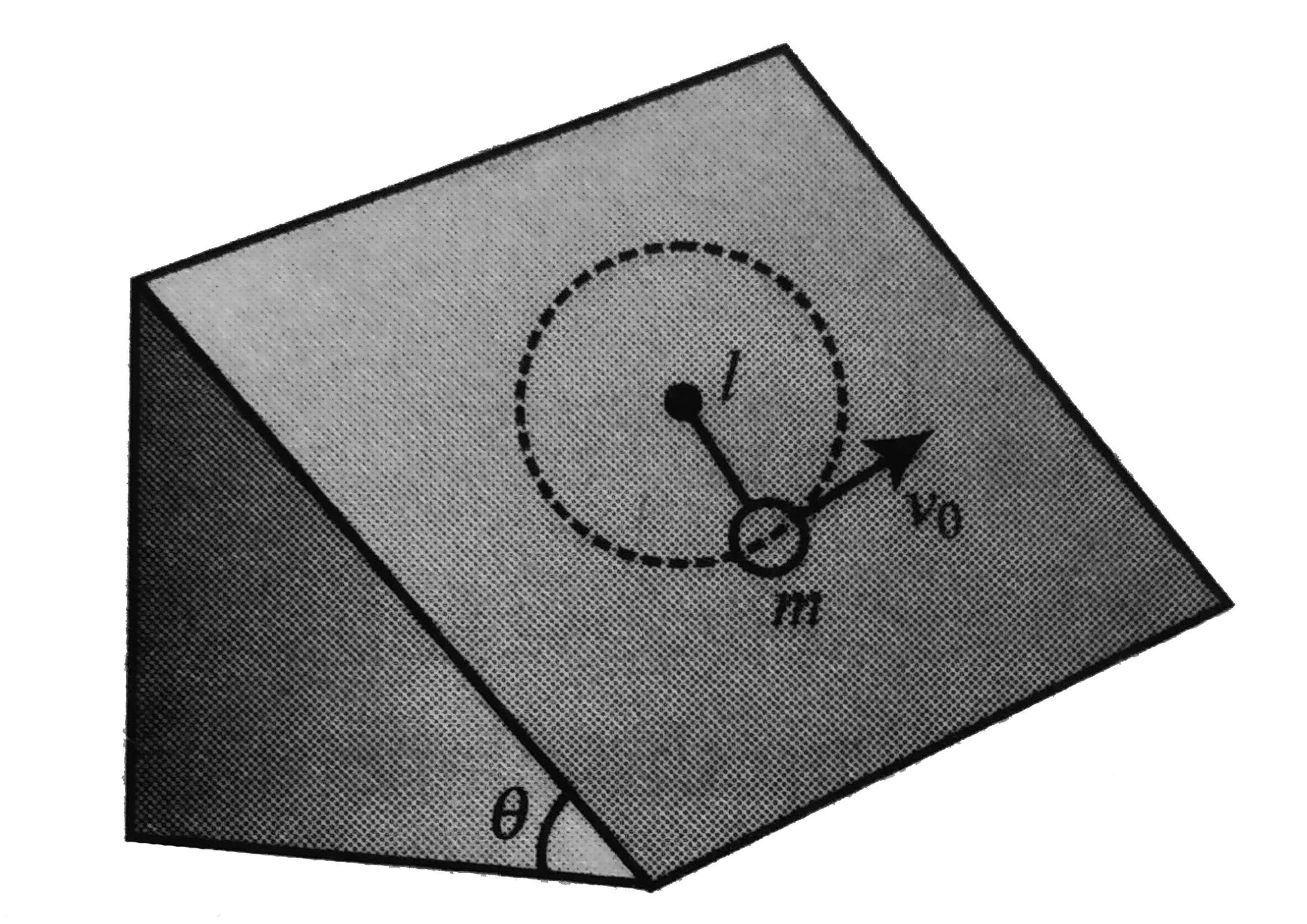
The speed of the bob at the highest point on the circle isView SolutionA pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where m=3kg, l=0.75m, θ=37∘. At the lowest point of the circle the tension in the string is T=274N. Take g=10ms−2.
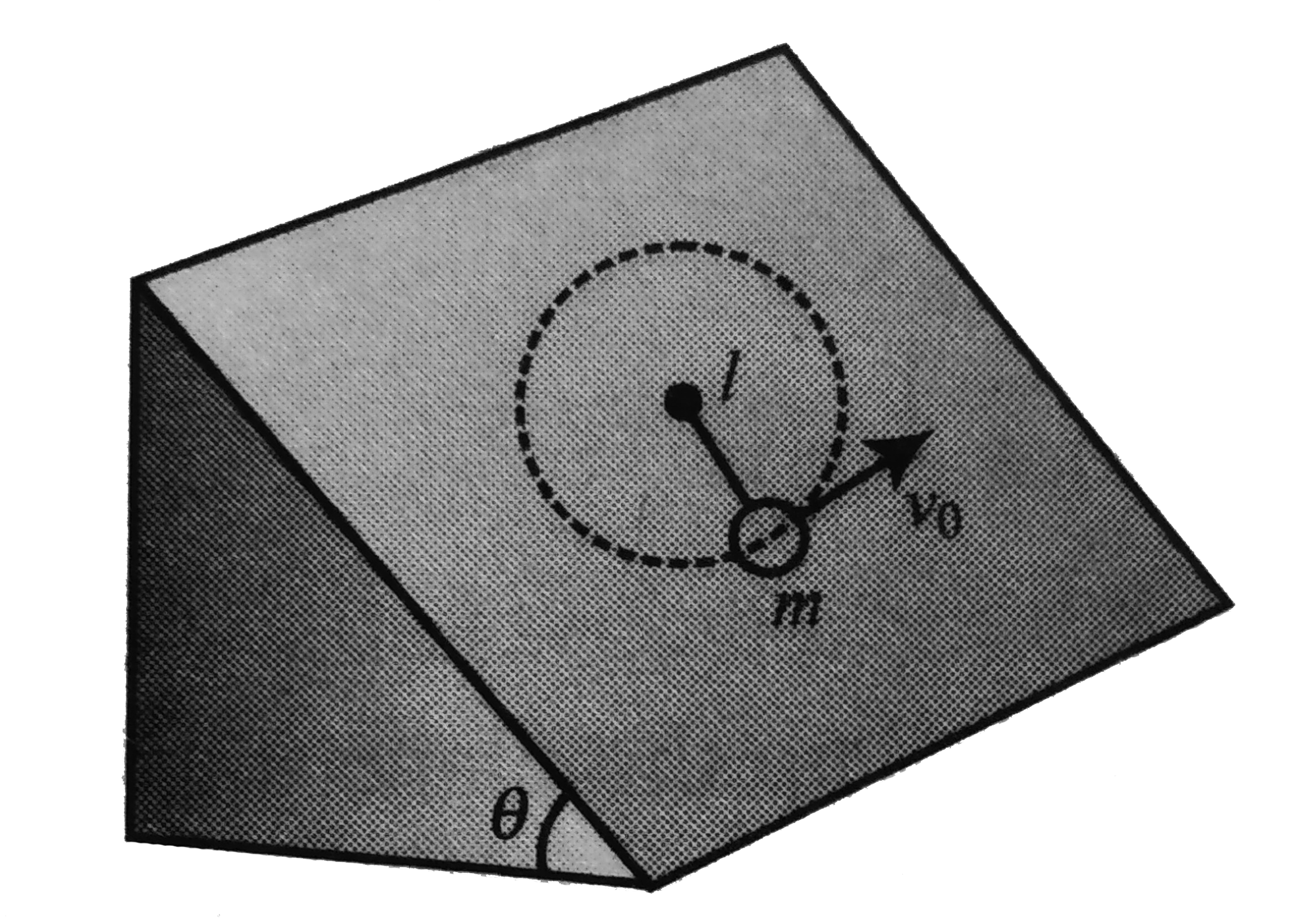
The speed of the bob at the lowest point isView SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string is T and acceleration of the particle is a at any position then T. a' is positive at the lowest point for
View SolutionA small spehre of mass m is connected by a stirng to a nail at O and moves in a circle of radius r on the smooth plane inclined at an angle θ with the horizontal. If the sphere has a velocity u at the top position A. Mark the correct options.
1)the tension in the string as the sphere passes the 90∘ position B is equal to m( u^2/l − 2gsinθ )
2)the tension in the string at the bottom most position C is equal to
m( u^2/l + 5gsinθ )
3)the tension in the string as the sphere passes the 90∘ position B is equal to m( u^2/l + 2gsinθ )
4)the tension in the string at the bottom most position C is equal to
m( u^2/l − 5gsinθ )
 View Solution
View SolutionA stone of 1 kg tied up with 10/3 m long string rotated in a vertical circle. If the ratio of maximum and minimum tension in string is 4 then speed of stone at highest point of circular path will be ( g=10ms2)
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u . The tension in the string T and acceleration of the particle is a at any position. Then T.a is zero at highest point if
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:
 View Solution
View SolutionA uniform string of length 10m and mass 20 kg lies on a smooth frictionless inclined plane. A force of 200N is applied as shown in the figure.

(a) Find the acceleration of the string.
(b) Find the tension in the string at 2m from end A.View SolutionSuppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
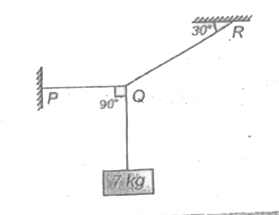 View Solution
View Solution

