A pendulum clock loses 12s a day if the temperature is 40∘C and gains 4s a day if the temperature is 20∘C, The temperature at which the clock will show correct time, and the co-efficient of linear expansion (α) of the metal of the pendulum shaft are respectively:
25∘C,α=1.85×10−5.∘C−1
60∘C,α=1.85×10−4.∘C−1
30∘C,α=1.85×10−3.∘C−1
55∘C,α=1.85×10−2.∘C−1
The correct Answer is:A
Time period of pendulum, T=2π√lg
ΔT=2π√g×12l−1/2Δl=πΔl√gl
∴ΔTT=πΔl/√gl2π√l/g=12Δll
When clock gains 12 s a day, then
12T=12α(40−θ) ....(i)
When clock gain loses 4 s a day, then
4T=12α(tˆa−20) ....(ii)
Dividing (i) by (ii) we get
3=40−θθ−20
or 3θ−60=40−θ or 4θ=100 or θ=25∘C
Putting this value of θ in (i), we get
12T=12α(40−25)=12α×15
or 1224×60×60=12α×15
or α=12×224×60×60×15=1.85×10−5.∘C−1
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Integer Type Questions
12 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Asseration - Reason Type Question
18 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
A pendulum clock loses 24 sec a day if the temperature is 60∘C and gains 8 sec a day if the temperature is 40∘C .The temperature at which the clock will show correct time.
View SolutionPendulum of a clock consists of very thin sticks of iron and an alloy. At room temperature the iron sticks 1 and 2 have length L0 each. Length of each of the two alloy sticks 4 and 5 is 0 and the length of iron stick 3 (measured up to the centre of the iron bob) is l0. Thickness of connecting strips are negligible and mass of everything except the bob is negligible. The pendulum oscillates about the horizontal axis shown in the figure. It is desired that the time period of the pendulum should not change even if temperature of the room changes. Find the coefficient of linear expansion (α) of the alloy if the coefficient of linear expansion for iron is α0.
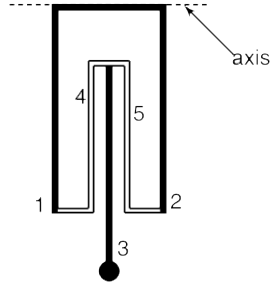
View Solution
Knowledge Check
A pendulam clock loses 12s a day if the temperature is 40∘C and gains 4s a day if the temperature is 20∘C, The temperature at which the clock will show correct time, and the co-efficient of linear expansion (α) of the metal of the pendulam shaft are respectively:
A30∘C:α=1.85×10−3/∘CB55∘C:α=1.85×10−2/∘CC25∘C:α=1.85×10−5/∘CD60∘C:α=1.85×10−4/∘CA pendulum clock is 5 sec. Slow at a temperature 30∘C and 10 sec. fast at a temperature of 15∘C, At what temperature does it give the correct time-
A18∘CB20∘CC25∘CDNone of theseA pendulum clock (fitted with a small heavy bob that is connected with a metal rod) is 5 seconds fast each day at a temperature of 15∘C and 10 seconds slow at a temperature of 30∘C. The temperature at which it is designed to give correct time, is
A18∘CB22∘CC20∘CD25∘C
A clock with a metallic pendulum gains 6 seconds each day when the temperature is 20∘C and loses 6 second when the temperature is 40∘C. Find the coefficient of linear expansions of the metal.
View SolutionA pendulum clock shows correct time at certain time at certain temperature. At a higher temperature the clock
View SolutionAn insulated chamber at a height h above the earth's surface and maintained at 30∘C has a clock fitted with an uncompensated pendulum. The maker of the clock for the chamber mistakenly design it to maintain correct time at 20∘C at that height. it is found that if the chamber were brought to earth's surface the clock in it would click correct time at 30∘C. the coefficient of linear expansion of the material of pendulum is (earth's radius is R)
View SolutionA clock with a metallic pendulum gains 5s each day at a temperature of 15∘C and loses 10s each day at a temperature of 30∘C. Find the coefficient of thermal expansion of the pendulum metal.
View SolutionA clock with a meta pendulum keeps correct time at 0∘C . If it loses 12.5 s a day at 25∘C , the coefficient of linear expansion of metal pendulum is
View Solution
