A pendulum comprising a light string of length L and small sphere, swings in the vertical plane . The string hits a peg located a distance of bellow the point of suspension (figure). If the pendulum is released from rest at the horizontal possition (θ=90∘) and is to swing in a complete circule centered on the peg, the minimum value of d is

L4
2L4
3L4
3L5
The correct Answer is:D
Energy is conserved in the swing of the pendulum , and the stationary peg does no work . So the ball's speed does nolt change when the string hits of leaveles
the peg and the ball swings equally high on both sides.
The ball will awing in a circule of radius R=(L−d) about the peg . If the ball is to travel in the circule, the minimum centripental acceleration at the top of the circule must be that of gravity:
mv2R=mg⇒v2=g(L−d)
When the ball is relaased from rest , Ui=mgL, and when it is at the top of the circle. Ui=mg2(L−d), where height is measered from the bottom of the swing. By energy conservation,
mgL=mg2(L−d)+12mv2
From this and the condition on v2 we final d=3L5
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Collision
31 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Problems Based On Mixed Concepts
32 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Mechanical Power
25 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
A pendulum, comprising a light string of length L and a small sphere, swings in a vertical plane. The string hits a peg located a distance d below the point of suspension as shown in the figure. If the pendulum is released from the horizontal position (θ=90∘) and is to swing in a complete circle centered on the peg, then the minimum value of d is kL. Find k :
'(##CEN_KSR_PHY_JEE_C07_012_Q06##)'
View SolutionA simple pendulum of length l and mass m free to oscillate in vertical plane. A nail is located at a distance d=l−a vertically below the point of suspension of a simple pendulum. The pendulum bob is released from the position where the string makes an angle of 90∘ from vertical. Discuss the motion of the bob if (a) l=2a and (b) l=2.5a.
View Solution
Knowledge Check
A simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is
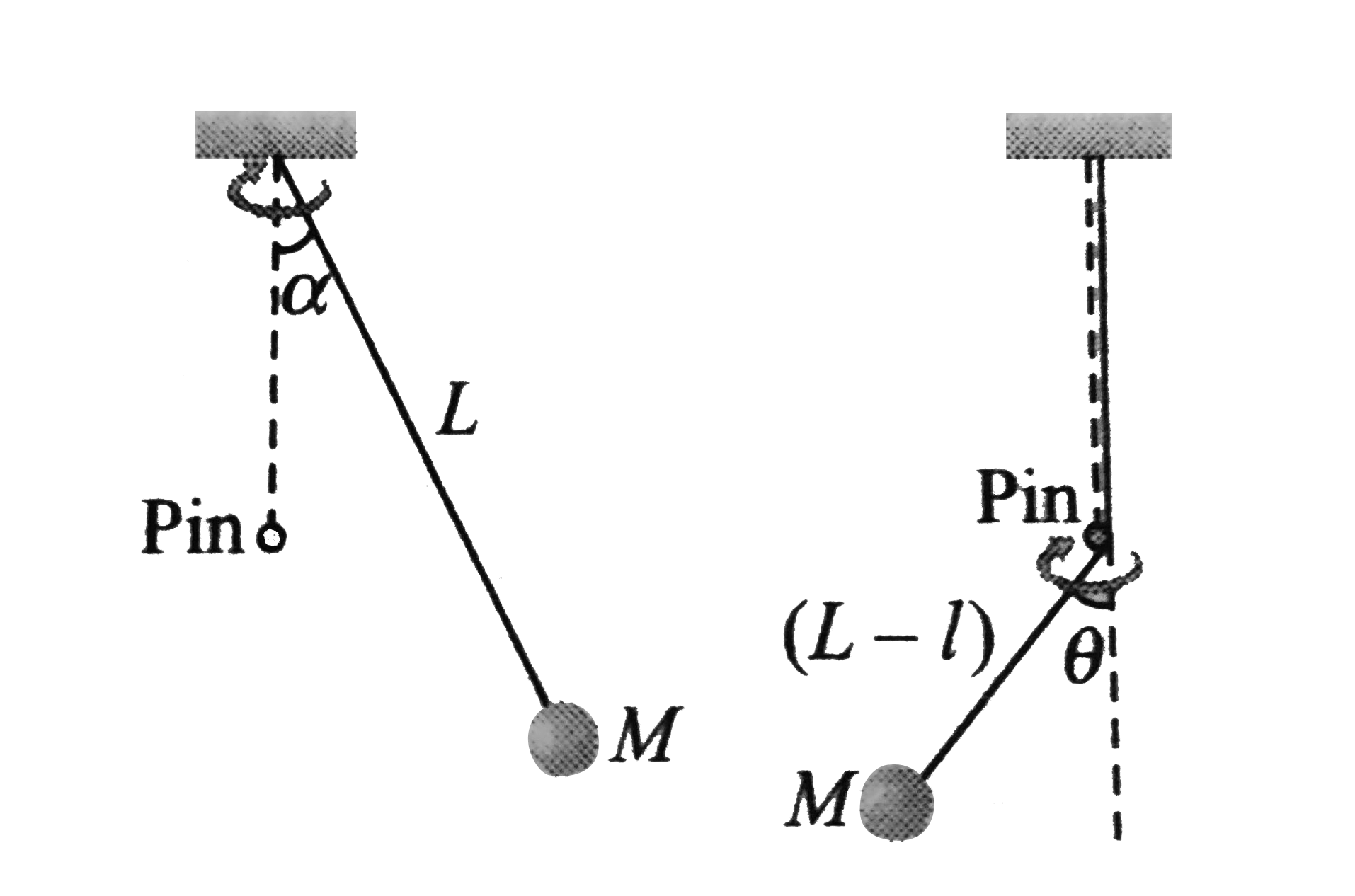 A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]
A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]A pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l4. The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
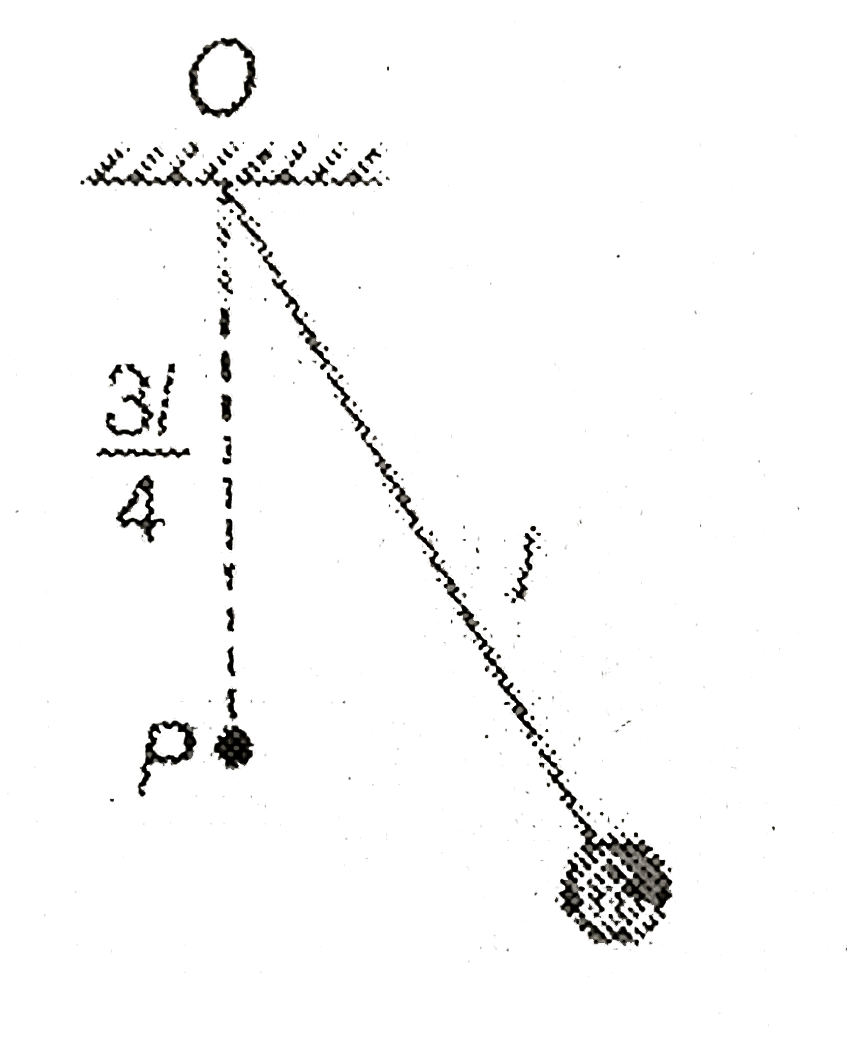 ATB3T4C3T5D4T5
ATB3T4C3T5D4T5
A simple pendulum of length L having a bob of mass m is first taken aside so that the string forms the tight angle with the verticle and then released. The string hits a peg which is fixed at a distance below the point of suspension and the bob starts going in a circle centered at the peg. find the minimum value of y for which the bob goes in a complete circle about the peg.

View SolutionIn the given system, when the ball of mass m is released, it will swing down the dotted circular are. A nail is located at a distance d below the point of suspension as shown in figure.
(a) How fast will it reach the lowest point in its swing?
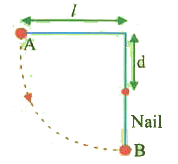
(b) Show that d must be at least 0.6l, if the ball is to swing completely around a circle centered along the nail.
(c) If d = 0.6 l, find the change in tension in the string just after it touches the nail.
View SolutionA bob tied to an ideal string of length l is released from the horizontal position shown. A peg P whose height is adjustable, can arrest the free swing of the pendulum, as shown in Figure.
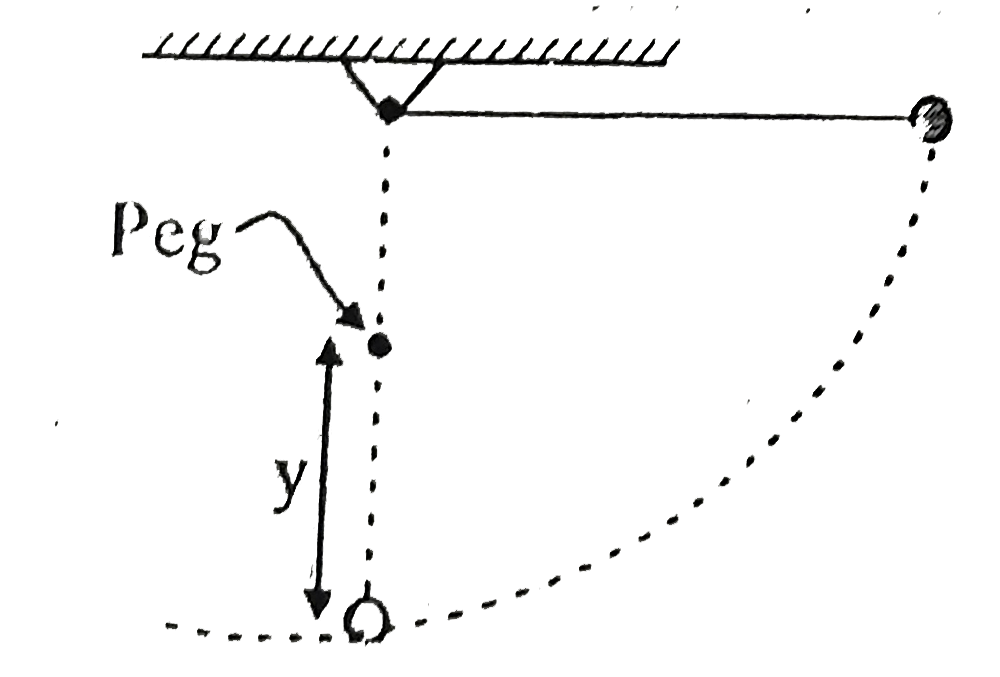
View SolutionA simple pendulum of length L having a bob of mass m is deflected from its rest position by an angle θ and released figure. The string hits a peg which is fixed at distance x below the point of suspension and the bob starts going in a circle centred at the peg. a. Assuming that initially the bob has a height less thasn the peg, show that the maximum height reached by the bob equals its initialheight. b. If the pendulum is released with θ=900 and m=L2 find the maximum height reached by the bob above its lowest positon before the string becomes slack. c. Find the minimum value of x/L for which the bob goes in a complete circle about the pet when the pendulum is released from θ=900.
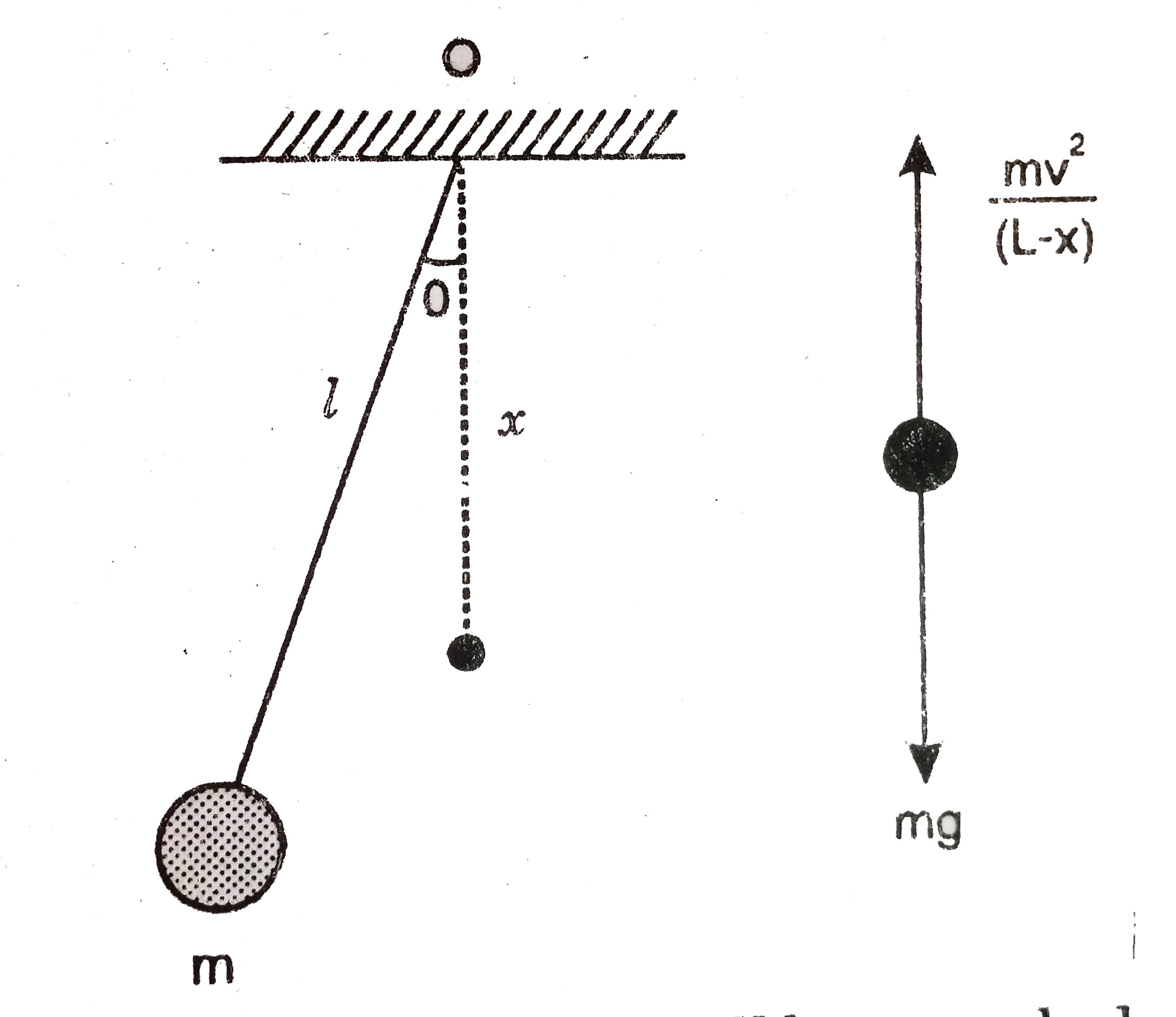
View SolutionThe bob of a simple pendulum of length l is released from a point in the same horizontal line as the point of suspension and at a distance l from it Calculate the tension in the string at the lowest point of its swing
(b) If the string of the pendulum is catched by a nail located verticaly below the point of suspensions and the bob just swings around a complete circle around the nail, find the distance of the nail from the point of suspension
(c) If the string of the pendulum is made of rubber then show that it will be stretched by 3 mg/k on reaching the bob at the lowest point. Here k is the force constant of the string
View SolutionA brass bob is suspended by an inextensible weightless string of length l from a peg fixed on a vertical wall. A nail is fixed in the wall at a distance d vertically below the point of suspension of the string. The bob is then drawn to a position where the string becomes horizontal and it is released from there. Show that d must be at least 0.6l if the bob is to swing completely around in a circle centred on the nail.
View Solution
