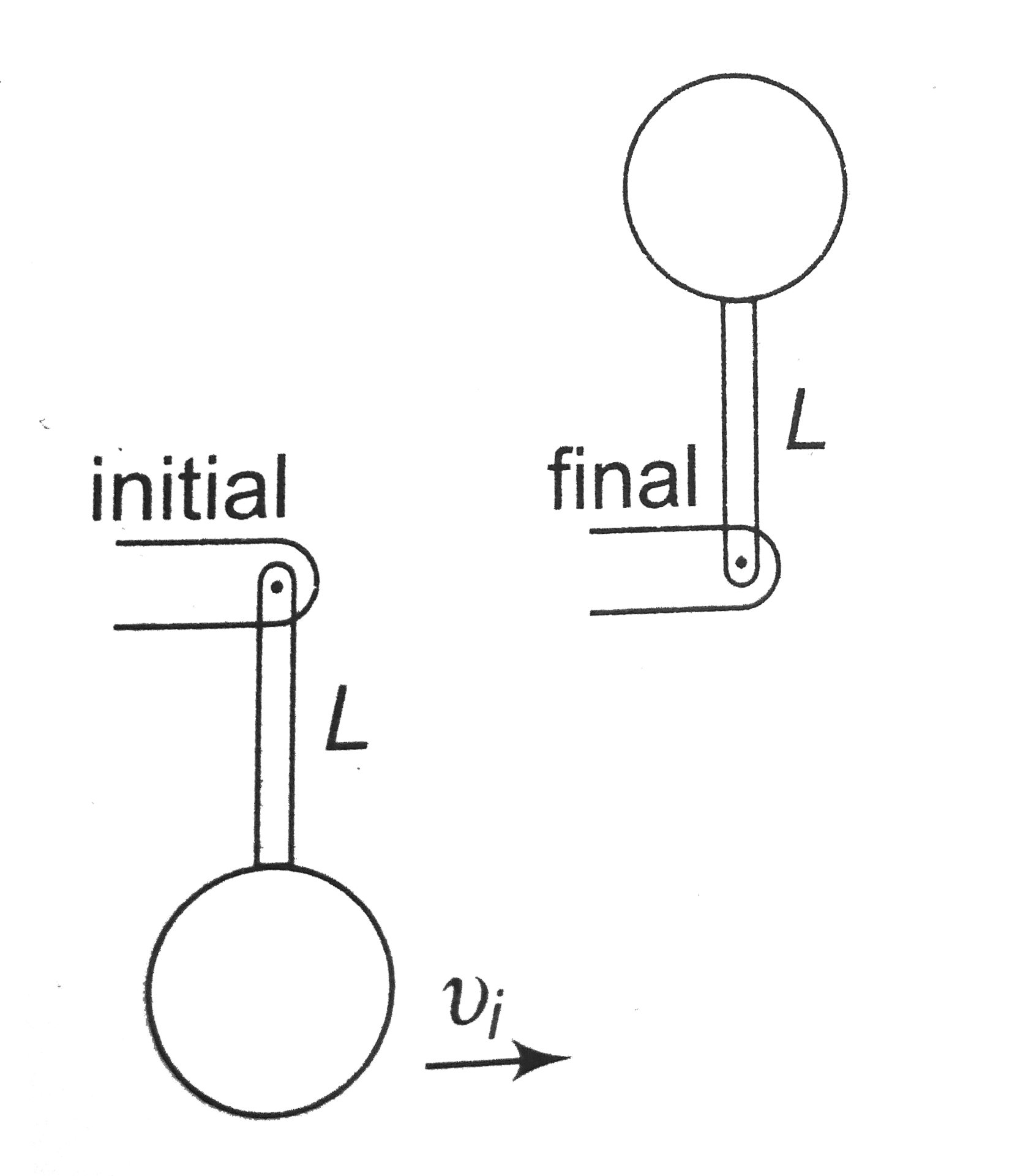
A light , right rod is 40.0cm long.Its top end is pivoted on a frictionless, horizontal axle. The rod hangs straight down at rest with a small , massive ball attached to its bottom end. You strike the ball, suddenly giving it a horizontal velocity so that it swings around in a full cirle. What minimum speed at the bottom is required to make the ball go over the top of the circle?
2.5m/s
4.0m/s
3.0m/s
5.0m/s
The correct Answer is:B
Consider energy conservation of the ball-Earth system beyween the instant just after you strike the ball and the instant when it reaches the rop . The speed as the top is zero if you hit it just hard enough to get it there.
ΔK=ΔU=0:
(0−12mv2i)+[mg(2L)−0]=0
vi=√4gL=√4(10.0m/s2)(0.40m)
vi=4.0m/s
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Collision31videos
WORK, ENERGY, POWER AND COLLISION
- BOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Problems Based On Mixed Concepts32videos
WORK, ENERGY, POWER AND COLLISION
- BOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Mechanical Power25videos
WORK, ENERGY, POWER AND COLLISION
- BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test30videos
WAVES AND ACOUSTICS
Similar Questions
A rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA ball rolls down an inclined trck 2 m long in 4s. Find speed of the ball at the bottom of the track.
View Solution
Knowledge Check
- Question 1 - Select One
A mass m is attached to the end of a rod of length l. The mass goes along a vertical circular path with the other end, hinged at its centre . What should be the minimum speed of mass at the bottom of this circular path
A√4glB√2glC√3glDNone of these - Question 2 - Select One
A ball attached to a string travels in uniform circular motion in a horizontal circle of 50 cm radius in 1 s. Sun light shining on the ball throws its shadow on a wall. The velocity of the shadow at the centre of the path is
Aπm/sB0.5πm/sC0.5m/sD1m/s - Question 3 - Select One
A ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?
A√glB√5glC√3glD√2gl
A rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.
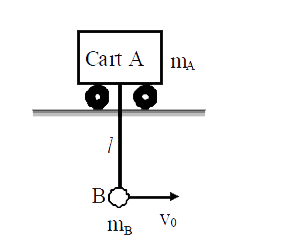
View SolutionA ball B is suspended from a string of length l attached to a cart A, which may roll on a frictionless surface. Initially the cart is at rest and the ball is given a horizontal velocity v0. Determine
the maximum height reached by the ball.
View SolutionOne end of a light rod is clamped in such a manner that rod can be rotated in a vertical plane . A block of mass mis attached to the other ened of rod and the block stays at rest at its lowest position . What minimum speed should be imparted to the bock so that it may complete its circle ? Assume length of rod to be l .
View SolutionTwo small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.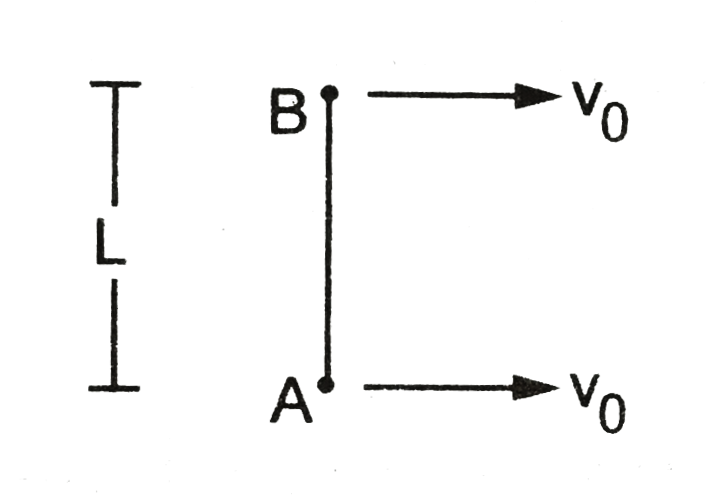
View SolutionA thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=mg2q. The rod is released from, shown position from rest.
What is the acceleration of the small ball at the instant of releasing the rod?View Solution