A pendulum with bob of mass is scillating on either side from its resting position A between the extremes B and Cala vertical height above A. What is the kinetic energy K and potential energy U when the pendulum is al positions (i) A. (ii) B. and (in C?
To solve the question regarding the kinetic energy (K) and potential energy (U) of a pendulum bob at different positions (A, B, and C), we can follow these steps:
1. Understanding the Positions:
- Position A: This is the lowest point of the swing where the pendulum is at rest.
- Position B: This is the highest point on one side of the swing.
- Position C: This is the highest point on the opposite side of the swing.
2. At Position A:
- At position A, the pendulum is at its lowest point.
- Here, the kinetic energy is at its maximum because the speed of the bob is highest.
- Potential energy is at its minimum (zero) because it is at the reference height.
- Kinetic Energy (K) = mgh (where h = 0 at A) = 0
- Potential Energy (U) = 0
3. At Position B:
- At position B, the pendulum is at its highest point on one side.
- Here, the kinetic energy is zero because the speed of the bob is zero at the peak.
- The potential energy is at its maximum because the bob has risen to a height (h) above the reference point A.
- Kinetic Energy (K) = 0
- Potential Energy (U) = mgh (where h is the height above A)
4. At Position C:
- At position C, the pendulum is at its highest point on the opposite side.
- Similar to position B, the kinetic energy is zero because the speed of the bob is zero at this peak.
- The potential energy is again at its maximum because the bob has risen to the same height (h) above the reference point A.
- Kinetic Energy (K) = 0
- Potential Energy (U) = mgh (where h is the height above A)
Summary of Energies at Each Position:
- At Position A:
- Kinetic Energy (K) = 0
- Potential Energy (U) = 0
- At Position B:
- Kinetic Energy (K) = 0
- Potential Energy (U) = mgh
- At Position C:
- Kinetic Energy (K) = 0
- Potential Energy (U) = mgh
- Position A: This is the lowest point of the swing where the pendulum is at rest.
- Position B: This is the highest point on one side of the swing.
- Position C: This is the highest point on the opposite side of the swing.
- At position A, the pendulum is at its lowest point.
- Here, the kinetic energy is at its maximum because the speed of the bob is highest.
- Potential energy is at its minimum (zero) because it is at the reference height.
- Kinetic Energy (K) = mgh (where h = 0 at A) = 0
- Potential Energy (U) = 0
- At position B, the pendulum is at its highest point on one side.
- Here, the kinetic energy is zero because the speed of the bob is zero at the peak.
- The potential energy is at its maximum because the bob has risen to a height (h) above the reference point A.
- Kinetic Energy (K) = 0
- Potential Energy (U) = mgh (where h is the height above A)
- At position C, the pendulum is at its highest point on the opposite side.
- Similar to position B, the kinetic energy is zero because the speed of the bob is zero at this peak.
- The potential energy is again at its maximum because the bob has risen to the same height (h) above the reference point A.
- Kinetic Energy (K) = 0
- Potential Energy (U) = mgh (where h is the height above A)
- At Position A:
- Kinetic Energy (K) = 0
- Potential Energy (U) = 0
- Kinetic Energy (K) = 0
- Potential Energy (U) = mgh
- Kinetic Energy (K) = 0
- Potential Energy (U) = mgh
Topper's Solved these Questions
- WORK ENERGY AND POWERBook:ICSEChapter: WORK ENERGY AND POWERExercise:EXERCISE-2(C )MULTIPLE CHOICE TYPE
Explore 2 Videos
- WORK ENERGY AND POWERBook:ICSEChapter: WORK ENERGY AND POWERExercise:EXERCISE-2(C ) NUMERICALS
Explore 6 Videos
- WORK ENERGY AND POWERBook:ICSEChapter: WORK ENERGY AND POWERExercise:EXERCISE-2(B) (NUMERICALS)
Explore 23 Videos
- CALORIMETRYBook:ICSEChapter:CALORIMETRYExercise:EXERCISE-11(B) (NUMERICALS)
Explore 15 Videos
Similar Questions
A pendulum is oscillating on either side of its rest position. Explain the energy changes that take place in the Oscillating pendulum. How does mechanical energy remain constant in it ? Draw the necessary diagram.
View SolutionThe figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
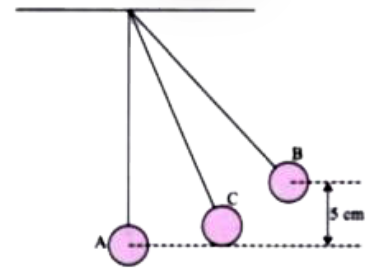
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)
View Solution
Knowledge Check
A ball of mass m is dropped from a cliff of height H. The ratio of its kinetic energy to the potential energy when it is fallen through a height 3/4 H is
A3:4B4:3C1:3D3:1
The amgular velocity and the amplitude of a simple pendulum is ω and a respectively. At a displacement x from the mean position, if its kinetic energy is T and potential energy is U, then the ratio of T to U is
View SolutionIn position A kinetic energy of a particle is 60 J and potential energy is -20 J. In position B, kinetic energy is 100 J and potential energy is 40 J. Then, in moving the particle from A to B
View SolutionAt what positions of the simple pendulum its (i) P.E. is maximum (ii) K.E. is zero ?
View SolutionIn the given question, let the charge be released from rest at point B. What will be its kinetic energy , when it crosses point A ?
View SolutionA satellite of mass 1000kg is supposed to orbit the earth at a height of 2000km above the earth's surface. Find a. its speed in the orbit b. its kinetic energy. c. The potential energy of the earth-satellite system and d. its time period. Mass of the earth =6×1024kg.
View SolutionA satellite of mass 1000 kg is supposed to orbit the earth at a height of 2000 km above the earth's surface. Find a). its speed in the orbit b). its kinetic energy. c). The potential energy of the earth satelilte system and d). its time period. Mass of the earth =6×1024kg.
View SolutionA simple pendulum with bob of mass m and length x is held in position at an angle θ1 and then angle θ2 with the vertical. When released from these positions, speeds with which it passes the lowest postions are v1&v2 respectively. Then ,v1v2 is.
View Solution