The amgular velocity and the amplitude of a simple pendulum is ω and a respectively. At a displacement x from the mean position, if its kinetic energy is T and potential energy is U, then the ratio of T to U is
(a2−x2ω2x2ω2)
x2ω2(a2−x2ω2)
(a2−x2)x2
x2(a2−x2)
The correct Answer is:C
To find the ratio of the kinetic energy (T) to the potential energy (U) of a simple pendulum at a displacement x from the mean position, we can follow these steps:
Step 1: Write the expression for Kinetic Energy (T)
The kinetic energy T of the pendulum can be expressed as:
T=12mω2(A2−x2)
where:
- m is the mass of the pendulum,
- ω is the angular velocity,
- A is the amplitude,
- x is the displacement from the mean position.
Step 2: Write the expression for Potential Energy (U)
The potential energy U of the pendulum at displacement x is given by:
U=12mω2x2
Step 3: Find the ratio of T to U
Now, we need to find the ratio TU:
TU=12mω2(A2−x2)12mω2x2
Step 4: Simplify the ratio
In this expression, the 12mω2 terms in the numerator and denominator cancel out:
TU=A2−x2x2
Final Answer
Thus, the ratio of kinetic energy to potential energy is:
TU=A2−x2x2
The kinetic energy T of the pendulum can be expressed as:
T=12mω2(A2−x2)
where:
- m is the mass of the pendulum,
- ω is the angular velocity,
- A is the amplitude,
- x is the displacement from the mean position.
The potential energy U of the pendulum at displacement x is given by:
U=12mω2x2
Now, we need to find the ratio TU:
TU=12mω2(A2−x2)12mω2x2
In this expression, the 12mω2 terms in the numerator and denominator cancel out:
TU=A2−x2x2
Thus, the ratio of kinetic energy to potential energy is:
TU=A2−x2x2
Similar Questions
The amplitude of a simple pendulum is 10 cm. When the pendulum is at a displacement of 4 cm from the mean position, the ratio of kinetic and potential energies at that point is
View SolutionIf A is amplitude of a particle in SHM, its displacement from the mean position when its kinetic energy is thrice that to its potential energy
View SolutionA particle executes shm of amplitude 'a'. (i) At what distance from the mean position is its kinetic energy equal to its potential energy? (ii) At what points is its speed half the maximum speed ?
View SolutionThe time period and the amplitude of a simple pendulum are 4 seconds and 0.20 meter respectively. If the displacement is 0.1 meter at time t=0, the equation on its displacement is represented by :-
View SolutionCalculate the ratio of displacement to amplitude when kinetic energy of a body is thrice its potential energy.
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm. At what distance from the mean position are the kinetic and potential energies equal?
View SolutionA particle performing SHM with amplitude 10cm. At What distance from mean position the kinetic energy of the particle is thrice of its potential energy ?
View SolutionThe magnitude of acceleration of a simple harmnic oscillator when its kinetic energy and potential energy are same, if amplitude of acceleration is a0 is
View SolutionThe figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
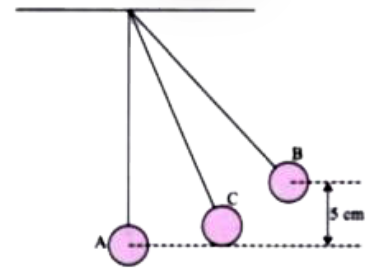
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)
View SolutionA body executes SHM with an amplitude a. At what displacement from the mean positions, the potentail energy of the body is one-fourth of its total energy?
View Solution
