A physical pendulum is positioned so that its centre of gravity is above the suspension point. When the pendulum is realsed it passes the point of stable equilibrium with an angular velocity ω. The period of small oscollations of the pendulum is
4πω
2πω
πω
π2ω
The correct Answer is:A
To find the period of small oscillations of a physical pendulum when its center of gravity is above the suspension point, we can follow these steps:
1. Understanding the System:
- A physical pendulum has its center of mass above the pivot point. When released, it passes through the point of stable equilibrium with an angular velocity ω.
2. Conservation of Energy:
- The kinetic energy (KE) of the pendulum at the point of stable equilibrium can be expressed as:
KE=12Iω2
- The potential energy (PE) at the maximum height (when the pendulum is at rest) can be expressed as:
PE=mgh=mg(2l)
where h=2l is the height of the center of mass above the pivot point.
3. Setting Kinetic Energy Equal to Potential Energy:
- By conservation of energy, we have:
12Iω2=mg(2l)
- Rearranging gives:
I=2mglω2
4. Using the Formula for the Period of a Compound Pendulum:
- The formula for the period T of a compound pendulum is given by:
T=2π√Imgl
5. Substituting for Moment of Inertia:
- Substitute I from step 3 into the period formula:
T=2π
⎷2mglω2mgl
6. Simplifying the Expression:
- The mgl terms cancel out:
T=2π√2ω2
- This simplifies to:
T=2π⋅√2ω
7. Final Result:
- Therefore, the period of small oscillations T is:
T=2√2πω
Conclusion:
The period of small oscillations of the pendulum is given by:
T=4πω
- A physical pendulum has its center of mass above the pivot point. When released, it passes through the point of stable equilibrium with an angular velocity ω.
- The kinetic energy (KE) of the pendulum at the point of stable equilibrium can be expressed as:
KE=12Iω2
- The potential energy (PE) at the maximum height (when the pendulum is at rest) can be expressed as:
PE=mgh=mg(2l)
where h=2l is the height of the center of mass above the pivot point.
- By conservation of energy, we have:
12Iω2=mg(2l)
- Rearranging gives:
I=2mglω2
- The formula for the period T of a compound pendulum is given by:
T=2π√Imgl
- Substitute I from step 3 into the period formula:
T=2π
⎷2mglω2mgl
- The mgl terms cancel out:
T=2π√2ω2
- This simplifies to:
T=2π⋅√2ω
- Therefore, the period of small oscillations T is:
T=2√2πω
The period of small oscillations of the pendulum is given by:
T=4πω
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
When the point of suspendion of pendulum is moved, its period of oscillation
View Solution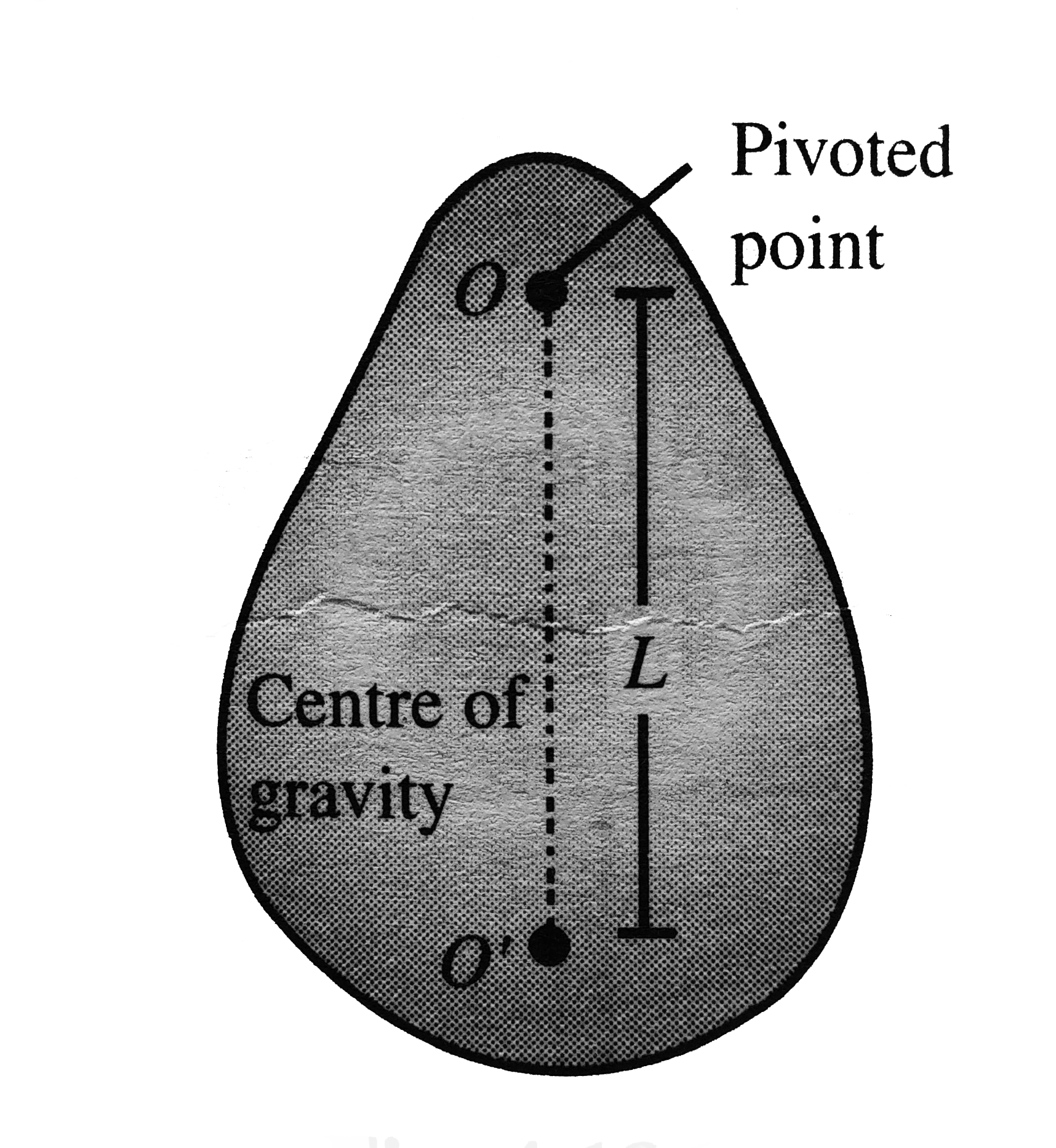
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.
View Solution
Knowledge Check
T=2π√Lg
The formula above was created by Italian scientist Galileo Galilei in the early 1600s to demonstrate that the time it takes for a pendulum to complete a swing-called its period, T-can be found using only the length of the pendulum, L, and the force of gravity, g He proved that the mass of the pendulum did not affect its period. Based on the equation above, which of the following equations could be used to find the length of the pendulum given its period ?AL=gT2πBL=gT24π2CL=T24π2gDL=g4π2T2
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. If an impulse J is applied at the centre of oscillation in the plane of oscillation, then angular velocity of the rod will be .

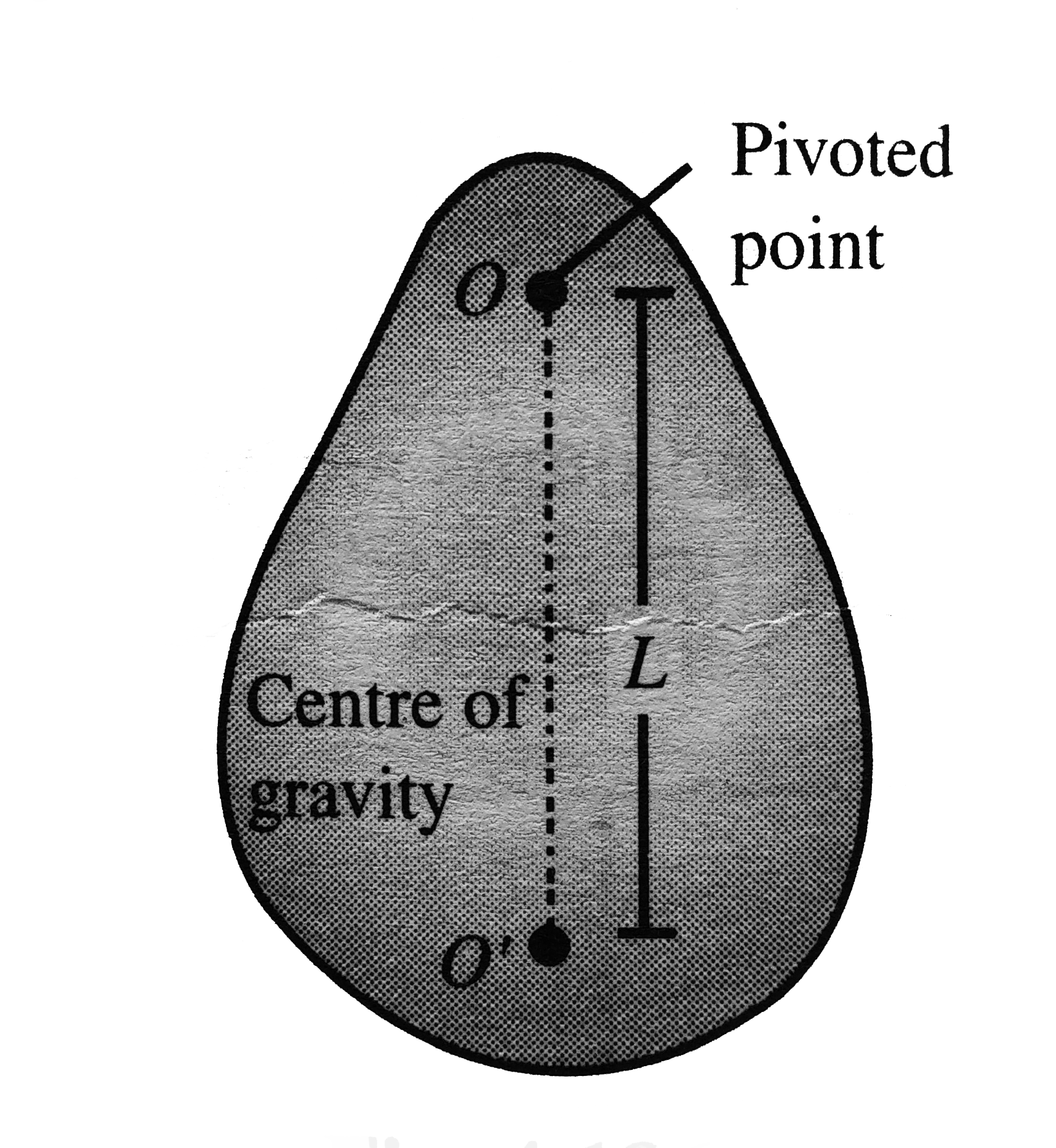
View SolutionIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. For the above question, locate the centre of oscillation.
View SolutionAn ideal pendulum was oscillating with an angular amplitude θ=π/3 inside a stationary elevator. When the pendulum was passing through equilibrium position, the lift suddenly starts moving upward with an acceleration a=g. Find the new angular amplitude of the oscillation.

View SolutionA simple pendulum of length l and mass m free to oscillate in vertical plane. A nail is located at a distance d=l−a vertically below the point of suspension of a simple pendulum. The pendulum bob is released from the position where the string makes an angle of 90∘ from vertical. Discuss the motion of the bob if (a) l=2a and (b) l=2.5a.
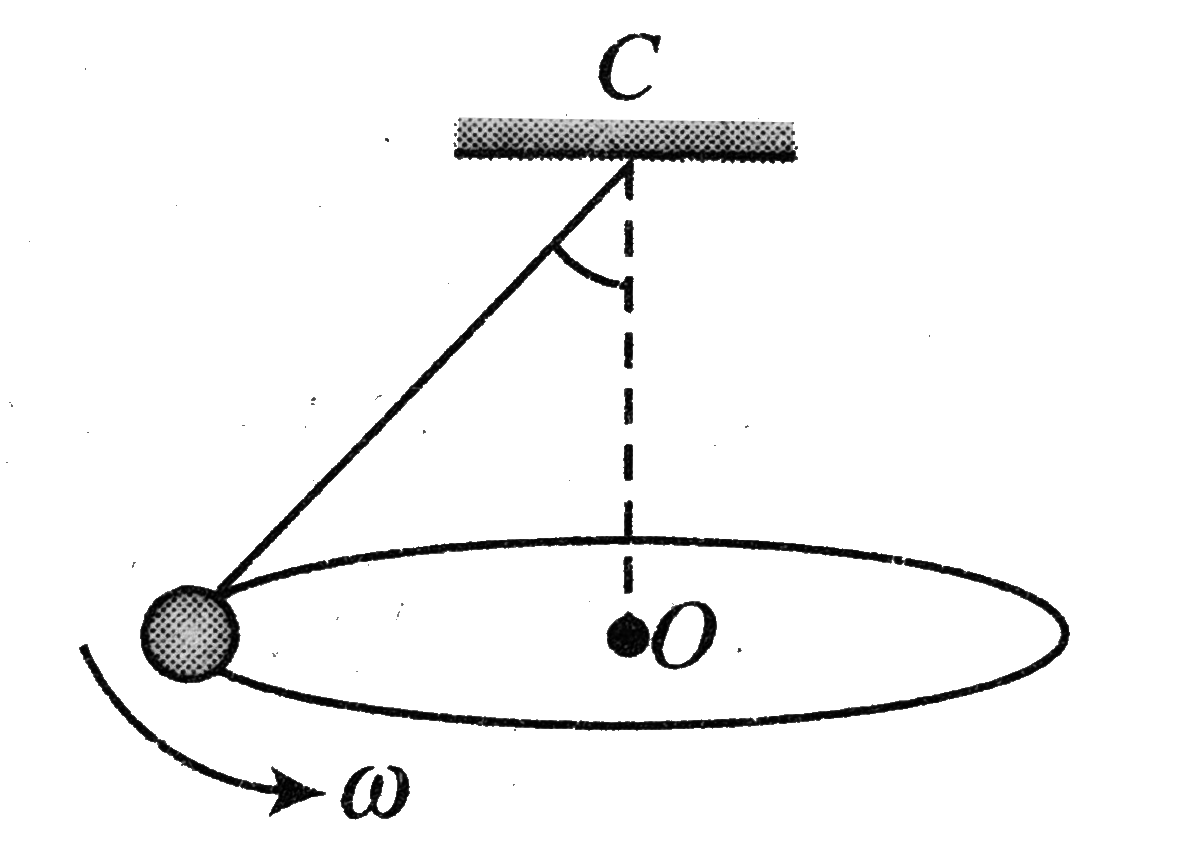
View SolutionA conical pendulum consists of a simple pendulum moving in a horizontal circle as shown in the figure. C is the pivot, O the centre of the circle in which the pendulum bob moves and ω the constant angular velocity of the bob. If →L is the angular momentum about point C, then
View SolutionStatement-1 : The motion of a simple pendulum is not simple harmonic for large amplitudes.
Statement-2 : The restoring torque on a simple pendulum about the point of suspension is proportional to sinθ, where θ is the angular displacement of the pendulum.
View SolutionA simple pendulum of length 1 oscillates aboμt the mean position as shown in the figure. If the total energy of the pendulum is E, the velocity of the pendulum bob of mass m at point P is:

View Solution
