A piece of uniform string hangs vertically so that its free end just touches horizontal surface of a table. The upper end of the string is now released. Show that at any instant during the falling of string, the total force on the surface is three times the weight of that part of string lying on the surface.
To solve the problem, we need to analyze the forces acting on the string and the table as the string falls. Let's break down the solution step by step.
Step 1: Define the Variables
Let:
- L = total length of the string
- m = mass per unit length of the string
- g = acceleration due to gravity
- x = length of the string that has fallen and is now lying on the table
- The weight of the string lying on the table at any instant is given by W=mgx.
Step 2: Analyze the Falling String
When the upper end of the string is released, it falls under the influence of gravity. At any instant, the length of the string that has fallen is x, and thus the length of the string lying on the table is also x.
Step 3: Calculate the Weight of the String on the Table
The weight of the string lying on the table at any instant is:
W=mgx
Step 4: Determine the Velocity of the Falling String
As the string falls a distance x, it acquires a velocity v. Using the equation of motion:
v2=u2+2as
where u=0 (initial velocity), a=g (acceleration), and s=x:
v2=0+2gx⟹v=√2gx
Step 5: Calculate the Rate of Change of Momentum
The momentum p of the falling string of length dx at any instant is given by:
p=mv=(m⋅dx)⋅v=m⋅dx⋅√2gx
The rate of change of momentum dpdt can be expressed as:
dpdt=m⋅dxdt⋅√2gx
Since dxdt=v, we can substitute v:
dpdt=m⋅v⋅√2gx=m⋅√2gx⋅√2gx=2mgx
Step 6: Calculate the Total Force on the Table
The total force F on the table at any instant is the sum of the weight of the string lying on the table and the rate of change of momentum:
F=mgx+dpdt=mgx+2mgx=3mgx
Conclusion
Thus, we have shown that at any instant during the falling of the string, the total force on the surface is three times the weight of the part of the string lying on the surface:
F=3mgx
Let:
- L = total length of the string
- m = mass per unit length of the string
- g = acceleration due to gravity
- x = length of the string that has fallen and is now lying on the table
- The weight of the string lying on the table at any instant is given by W=mgx.
When the upper end of the string is released, it falls under the influence of gravity. At any instant, the length of the string that has fallen is x, and thus the length of the string lying on the table is also x.
The weight of the string lying on the table at any instant is:
W=mgx
As the string falls a distance x, it acquires a velocity v. Using the equation of motion:
v2=u2+2as
where u=0 (initial velocity), a=g (acceleration), and s=x:
v2=0+2gx⟹v=√2gx
The momentum p of the falling string of length dx at any instant is given by:
p=mv=(m⋅dx)⋅v=m⋅dx⋅√2gx
The rate of change of momentum dpdt can be expressed as:
dpdt=m⋅dxdt⋅√2gx
Since dxdt=v, we can substitute v:
dpdt=m⋅v⋅√2gx=m⋅√2gx⋅√2gx=2mgx
The total force F on the table at any instant is the sum of the weight of the string lying on the table and the rate of change of momentum:
F=mgx+dpdt=mgx+2mgx=3mgx
Thus, we have shown that at any instant during the falling of the string, the total force on the surface is three times the weight of the part of the string lying on the surface:
F=3mgx
Similar Questions
A very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
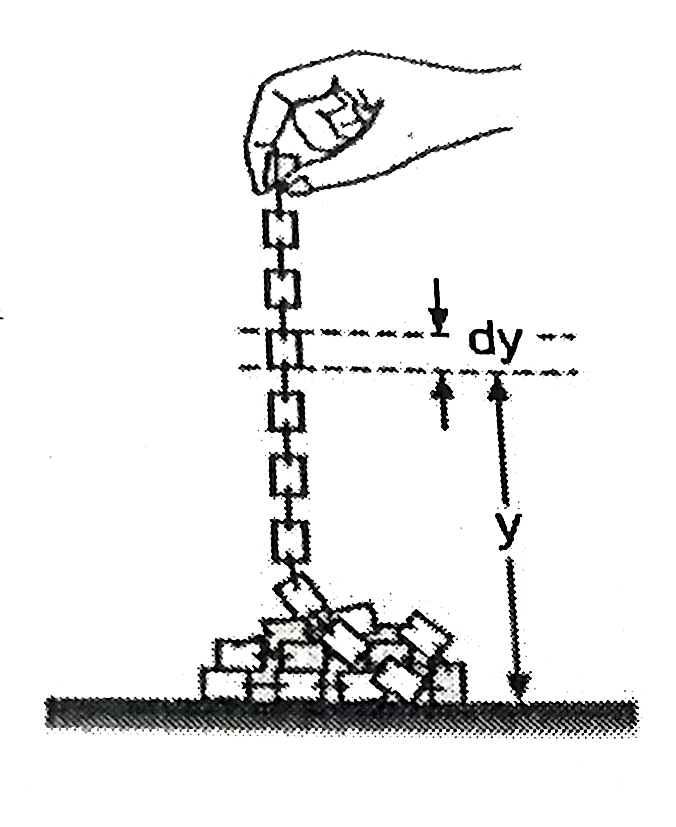
View SolutionA uniform rope of mass m per unit length, hangs vertically from a support so that the lower end just touches the table top shown in figure. If it is released, show that at the time a length y of the rope has fallen, the force on the table is equivalent to the weight of the length 3y of the rope.

View SolutionA perfectly elastic uniform string is suspended vertically with its upper end fixed to the ceiling and the lower end loaded with the weight. If a transverse wave is imparted to the lower end of the string, the pulse will
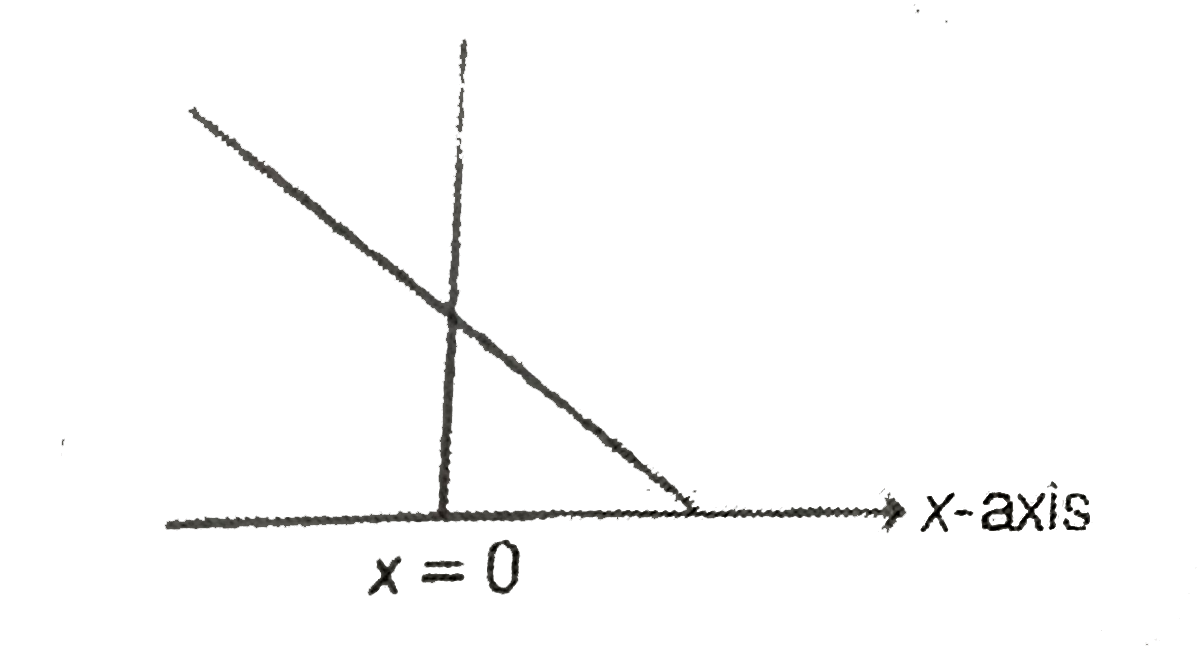
View SolutionA uniform rod of length l is kept vertically on a rough horizontal surface at x = 0 . It is rotated slightly and released . When the rod finally falls on the horizontal surface , the lower end will remain at
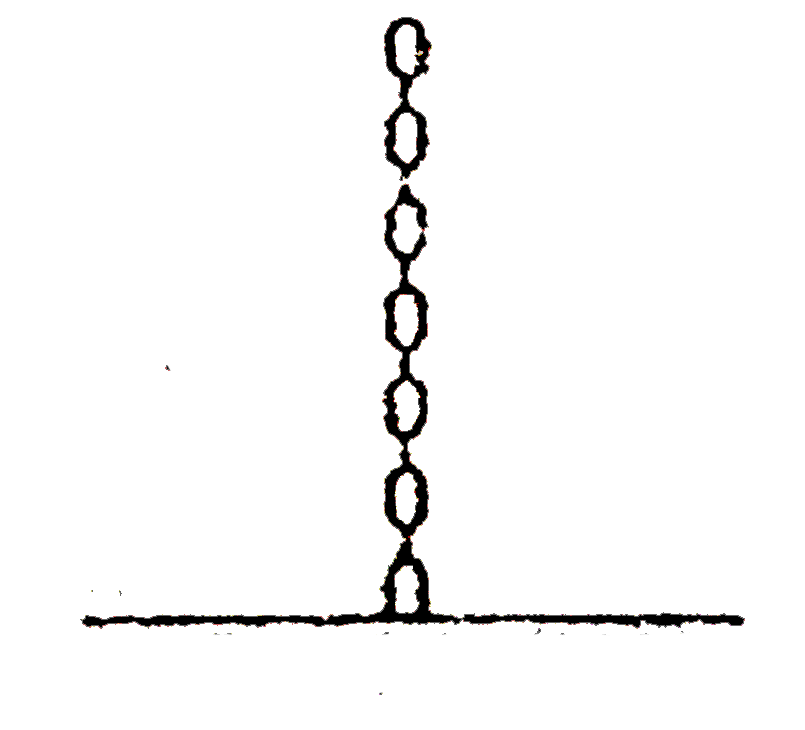
View SolutionA uniform chain of mass m and length l hanges on a thread and touches the surface of a table by its lower end. Find the force exerted by the table on the chain when half of its length has fallen on the table. The fallen part does not form heap.

View SolutionA uniform chain of mass m and length l hangs on a thread and touches the surface of a table by its lower end. Thread breaks suddenly. Find the force exerted by the table on the chain when half of its length has fallen on the table. The fallen part does not form heap
View SolutionA uniform rod is kept vertically on a horizontally smooth surface at a point O. IF it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain
View SolutionA particle A of mass 2m is held on a smooth horizontal table and is attached to one end of an inelastic string which runs over a smooth light pulley at the edge of the table. At the other end of the string there hangs another particle B of mass m, the distance from A to the pulley is l. The particle A is then projected towards the pulley with velocity u.

(a) Find the time before the string becomes taut, and shown that after the string becomes taut, the initial velocity of A and B is 4u/3.
(b) Find the common velocity when A reaches the pulley (assume that B has not yet reached the ground).
View SolutionWedge of 10kg is free to move on horizontal surface. At the given instant, acceleration of wedge is (string and pulleys are ideal)
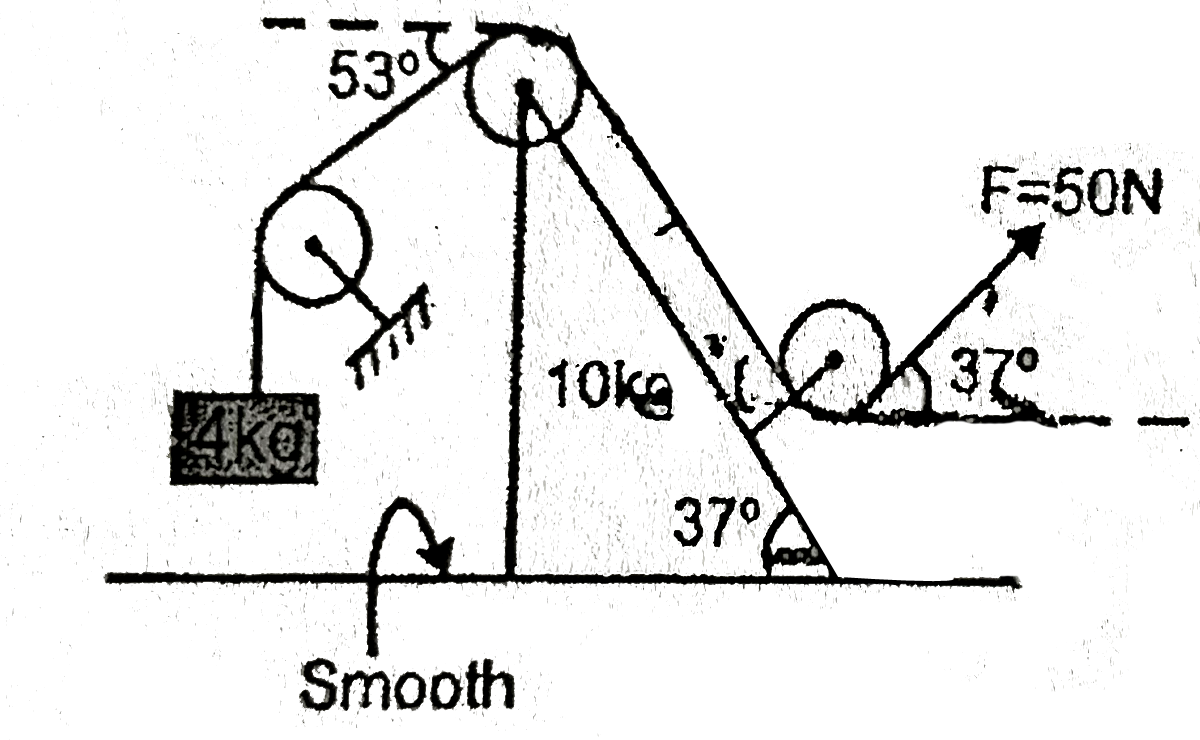
View SolutionA disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
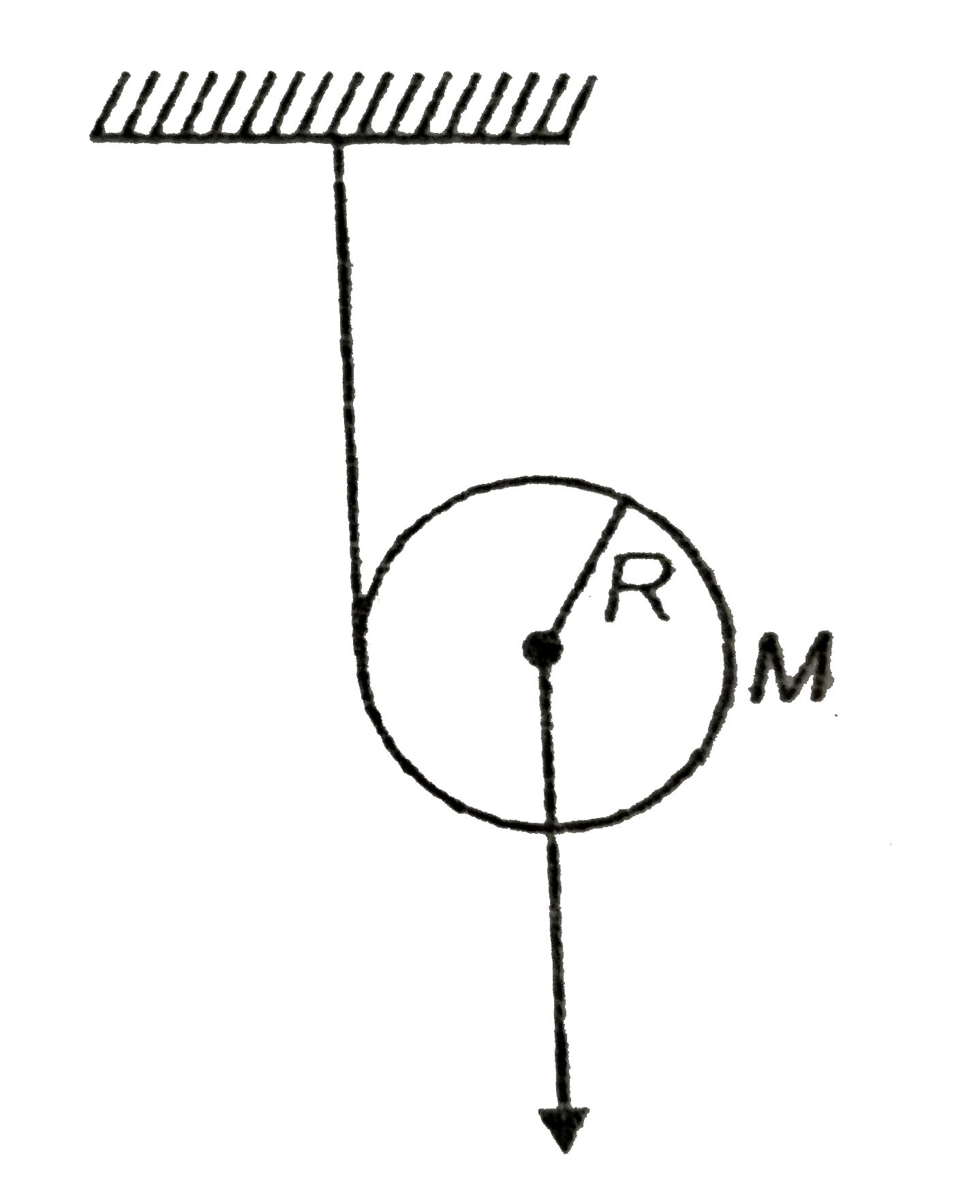
View Solution
