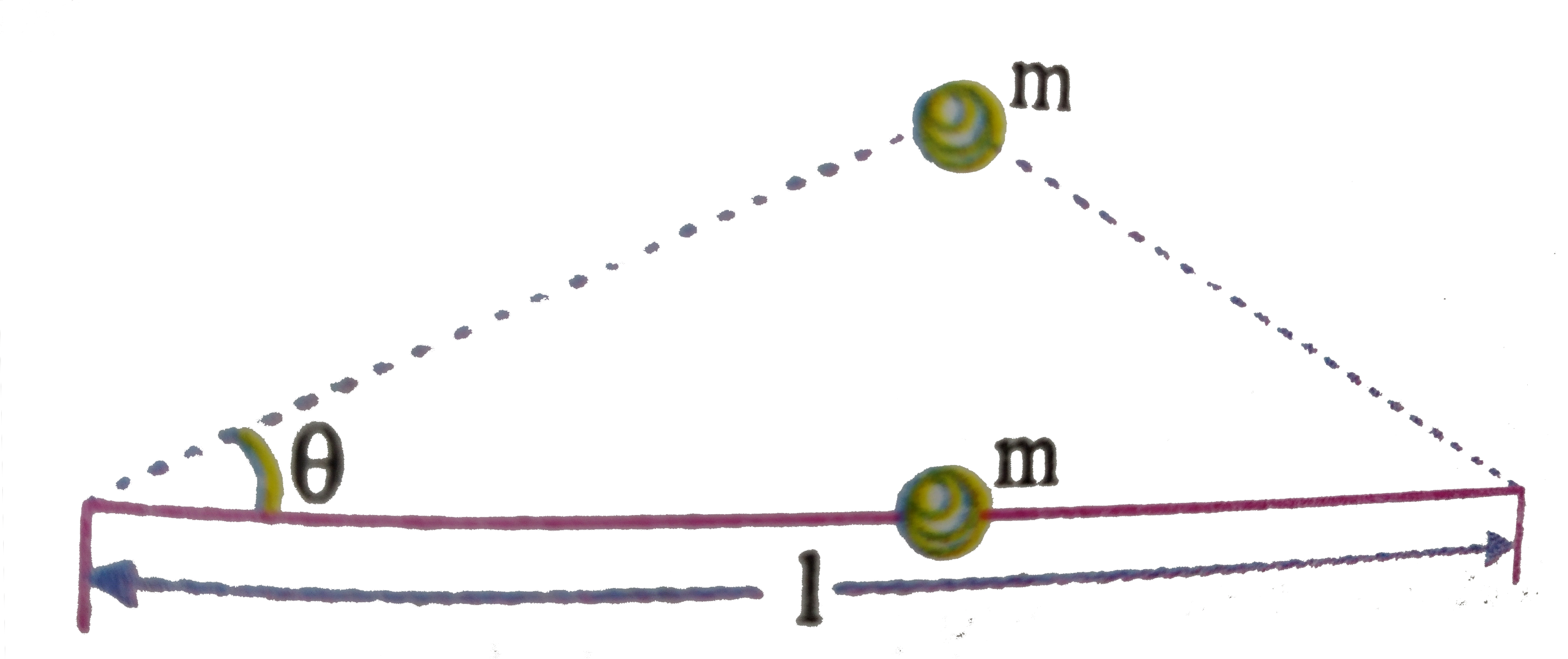
A string secured at its ends is stretched with a force of tension F. The mass of the string and the force of gravity can be neglected. A point weight with a mass m is attached to the middle of the string. The time period of small oscillations of the weight is 2π√mlxF. the value of x is ________
(Neglect any change in the magnitude of tension of the string during oscillations)
The correct Answer is:4
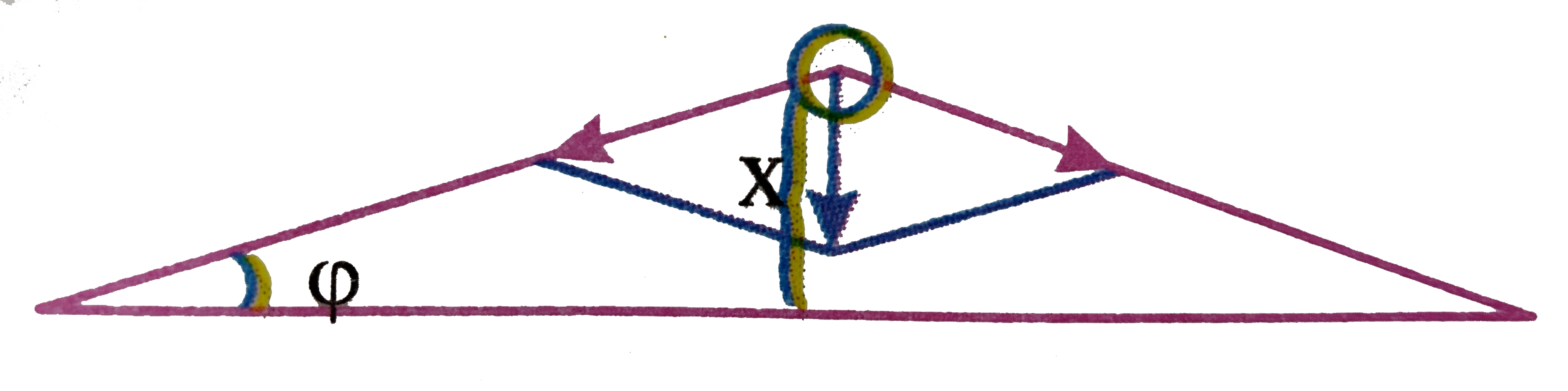
The force acting on the weight delected from the position of equilibrium is 2Fsinϕ Since the angle ϕ is small, it may be assumed that
Force =4FxlorF=kx, where k=4Fl. By using the formula T=2π√mk
We get the following expression for the sough quantity: T=2π√ml4F
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-I (H.W)
1 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DISPLACEMENT
6 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-XIII
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
The block shown in figure has a mass M and descends with an acceleration a. the mass of the string below the point A is m. Find the tension of the string at the point A and at the lower end.

View SolutionA bird with mass m parches at the middle of a strectched string Show that the tension in the string is give by T=mg2sinθ. Assuming that each half of the string is straight.

View Solution
Knowledge Check
Force of friction and tension in a string are
AGravitational forcesBElectromagnetic forcesCNuclear forcesDWeal forcesForce of friction and tension in a string are
AGravitational forcesBElectromagnetic forcesCNuclear forcesDWeal forcesThe block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mg
The block is placed on a frictionless surface in gravity free space. A heavy string of a mass m is connected and force F is applied on the string, then the tension at the middle of rope is

View SolutionThe block is placed on a frictionless surface in gravity free space. A heavy string of a mass m is conncected and force F is applied on the string then the tension at the middle of rope is
 .
.
View SolutionA bead of mass m is attached to the mid-point of a taut, weightless string of length l and placed on a frictionless horizontal table.
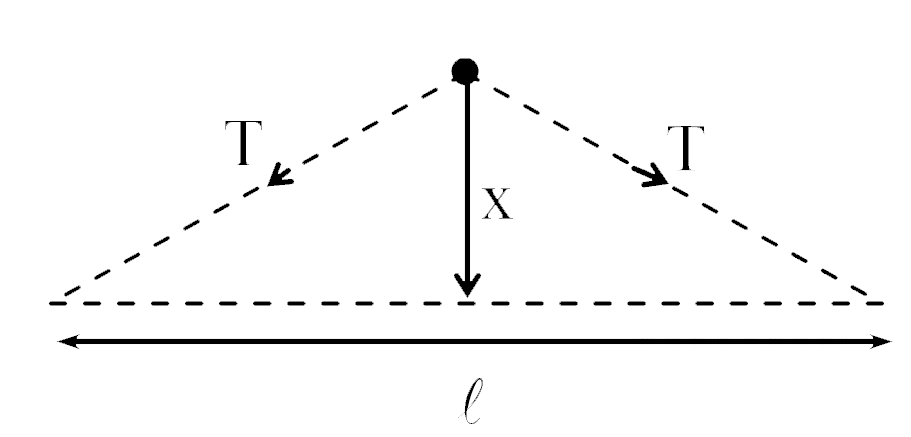
Under a small transverse displacement x, as shown, if the tension in the string is T, then the frequency of oscillation is-
View SolutionTwo bodies of masses 4kg and 6kg are attached to the ends of a string which passes over a pulley, the 4kg mass is attached to the table top by another string.The tension in this string T1 is equal to
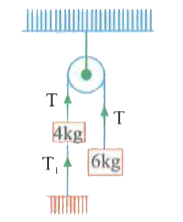
View SolutionTwo bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
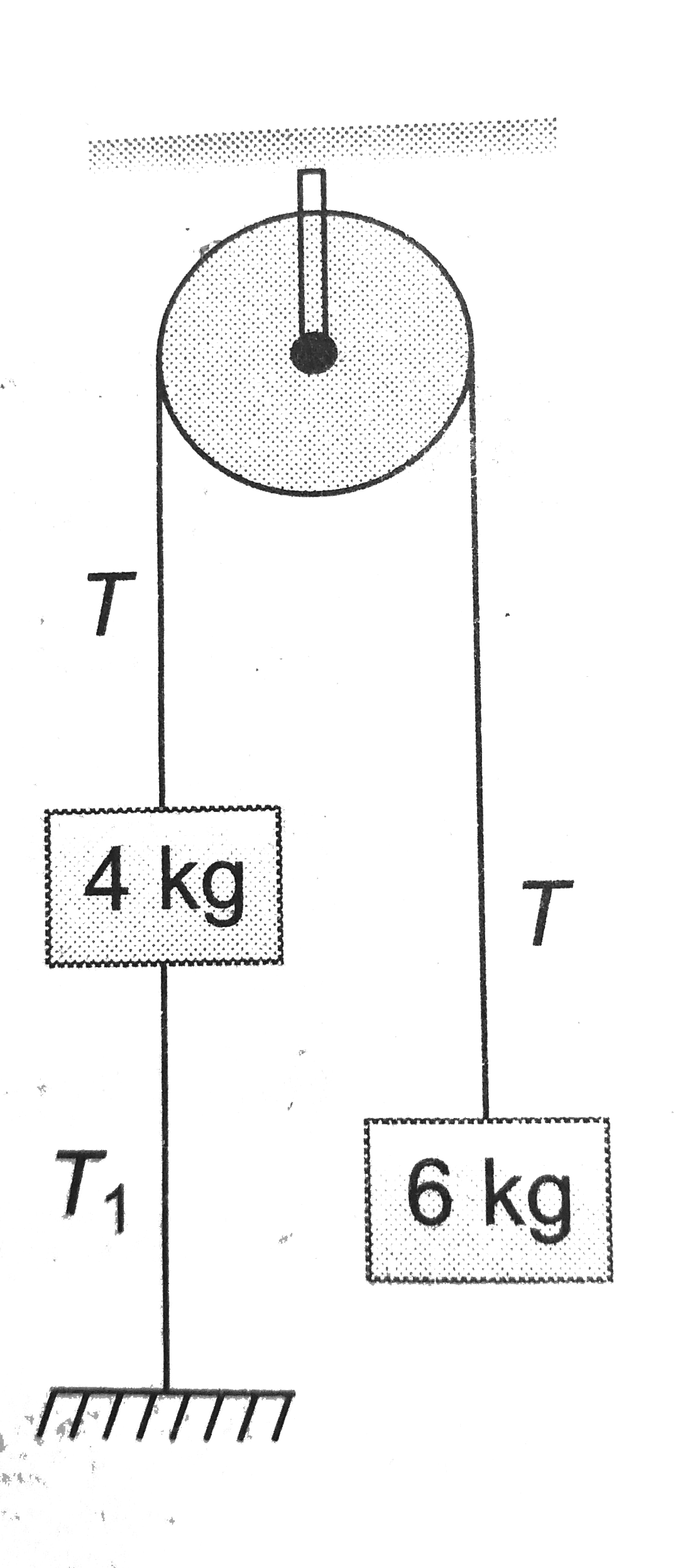
View Solution
