A plane is flying at a speed of with respect to air. The wind is blowing at a speed of from west to east. With respect to ground the plane is found to be movig northwards. In which direction is the plane heading?
North-West at angle to north
North-West at angle to west.
North-East at angle to north.
North -East at angle to east
The correct Answer is:D
To solve the problem, we need to analyze the motion of the plane and the wind vector. We will use vector addition to determine the direction in which the plane is heading.
1. Identify the Given Information:
- Speed of the plane with respect to air, Vpa=720km/h
- Speed of the wind from west to east, Vw=54km/h
- Resultant motion of the plane with respect to the ground is northward.
2. Draw the Vectors:
- Represent the wind vector Vw pointing east.
- Represent the plane's velocity vector Vpa at an angle θ with respect to the north direction.
3. Set Up the Vector Components:
- The plane's velocity can be broken down into two components:
- Northward component: VpN=Vpacos(θ)
- Eastward component: VpE=Vpasin(θ)
4. Use the Wind's Effect:
- Since the resultant motion of the plane is northward, the eastward component of the plane's velocity must equal the wind's velocity:
VpE=Vw
- Therefore, we have:
Vpasin(θ)=54km/h
5. Substitute the Known Values:
- Substitute Vpa=720km/h into the equation:
720sin(θ)=54
6. Solve for sin(θ):
- Rearranging gives:
sin(θ)=54720=340
7. Find the Angle θ:
- To find θ, take the inverse sine:
θ=sin−1(340)
8. Determine the Direction:
- Since the plane is heading northwest (to counteract the eastward wind), the final heading of the plane is northwest at an angle θ from the north.
Final Answer:
The plane is heading northwest at an angle of sin−1(340) to the north.
- Speed of the plane with respect to air, Vpa=720km/h
- Speed of the wind from west to east, Vw=54km/h
- Resultant motion of the plane with respect to the ground is northward.
- Represent the wind vector Vw pointing east.
- Represent the plane's velocity vector Vpa at an angle θ with respect to the north direction.
- The plane's velocity can be broken down into two components:
- Northward component: VpN=Vpacos(θ)
- Eastward component: VpE=Vpasin(θ)
- Since the resultant motion of the plane is northward, the eastward component of the plane's velocity must equal the wind's velocity:
VpE=Vw
- Therefore, we have:
Vpasin(θ)=54km/h
- Substitute Vpa=720km/h into the equation:
720sin(θ)=54
- Rearranging gives:
sin(θ)=54720=340
- To find θ, take the inverse sine:
θ=sin−1(340)
- Since the plane is heading northwest (to counteract the eastward wind), the final heading of the plane is northwest at an angle θ from the north.
The plane is heading northwest at an angle of sin−1(340) to the north.
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
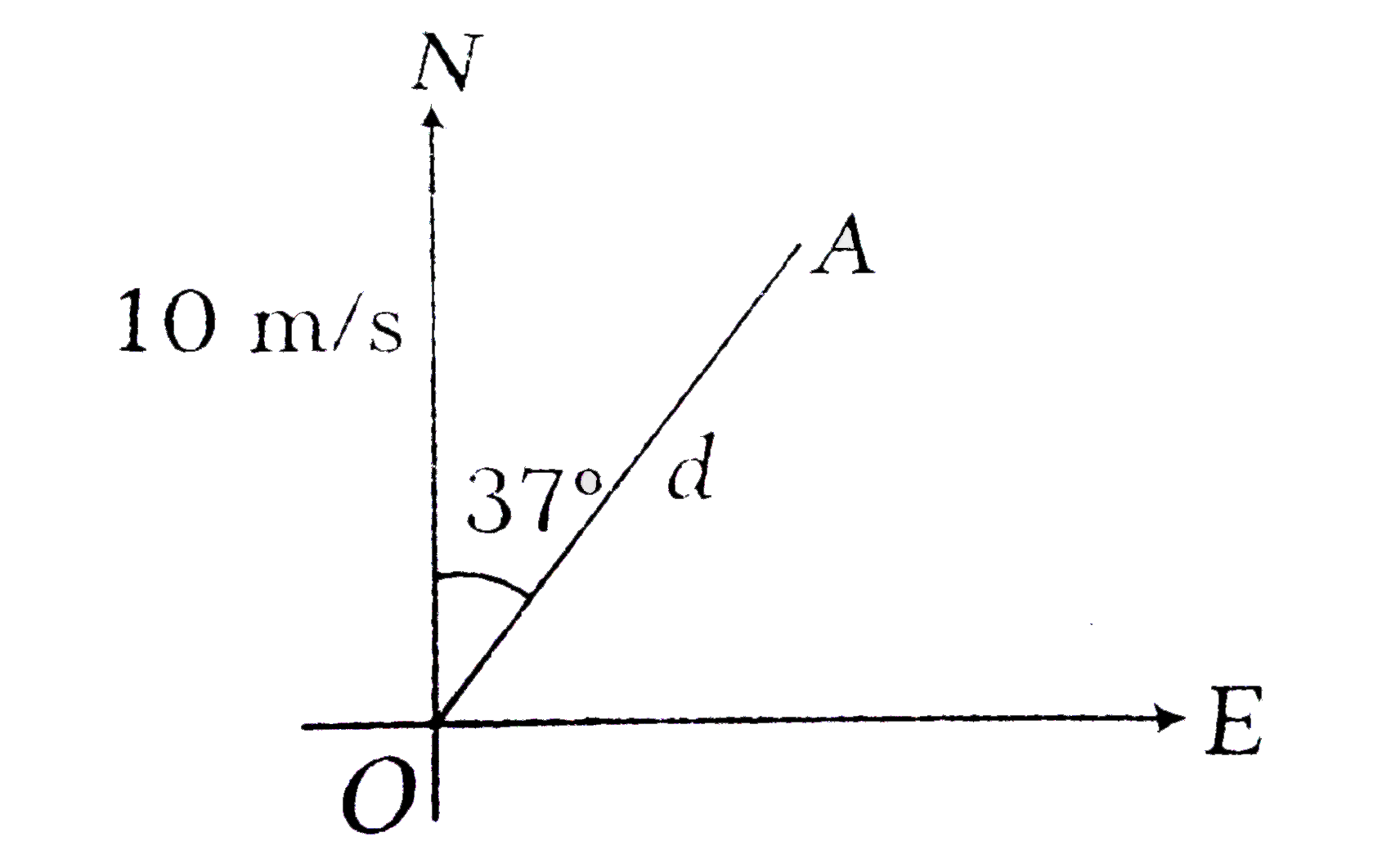
An aeroplane has to go from a point O to another point A, at distance d due 37∘ East of North. A wind is blowing due North at a speed of 10ms−1. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
View SolutionAn aeroplane is flying with a velocity 800kmph relative to air wind is belong from west to east with a velocity 15ms−1. Find velocity of aeroplane relative to the earth to fly south ward
View Solution
Knowledge Check
Rain is falling vertically with a speed of 30ms−1 . A woman rides a bicycle with a speed of 12ms−1 in east to west direction. In which direction should she hold her umbrella ?
AAt an angle of tan−1(25) with the vertical towards the east.BAt angle of tan−1(25) with the vertical towards the west.CAt angle of tan−1(52) with the vertical towards the westDAt angle of tan−1(52) with the vertical towards the west.Rain is falling vertically with a speed of 35ms−1 . A woman rides a bicycle with a speed of 12ms−1 in east to west direction. In which direction should she hold her umbrella ?
Asin−1(1235)Bcos−1(1235)Ctan−1(1235)Dcot−1(1235)A jet airplane travelling at the speed of 500km−1 ejects its products of combustion at the speed of 1500kmh−1 relative to the jet plane. What is the speed of the burnt gases with respect to observer on the ground ?
A500kmh−1B1000kmh−1C1500kmh−1D2000kmh−1
Rain is falling vertically with a speed of 1ms−1 . A woman rides a bicycle with a speed of 1.732 ms−1 in east to west direction. What is the direction in which she should hold her umbrella ?
View SolutionRain is falling vertically with a speed of 35ms−1. A woman rides a bicycle with a speed of 12ms−1 in east to west direction. What is the direction in which she should hold her umbrella?
View SolutionRain is falling vertically with a speed of 35ms−1 . A woman rides a bicycle with a speed of 12ms−1 in east to west direction. In which direction should she hold her umbrella ?
View SolutionRain is falling vertically with a speed of 35ms−1 . A woman rides a bicycle with a speed of 12ms−1 in east to west direction. In which direction should she hold her umbrella ?
View SolutionA jet airplane travelling at the speed of 500km−1 ejects its products of combustion at the speed of 1500kmh−1 relative to the jet plane. What is the speed of the burnt gases with respect to observer on the ground ?
View Solution
