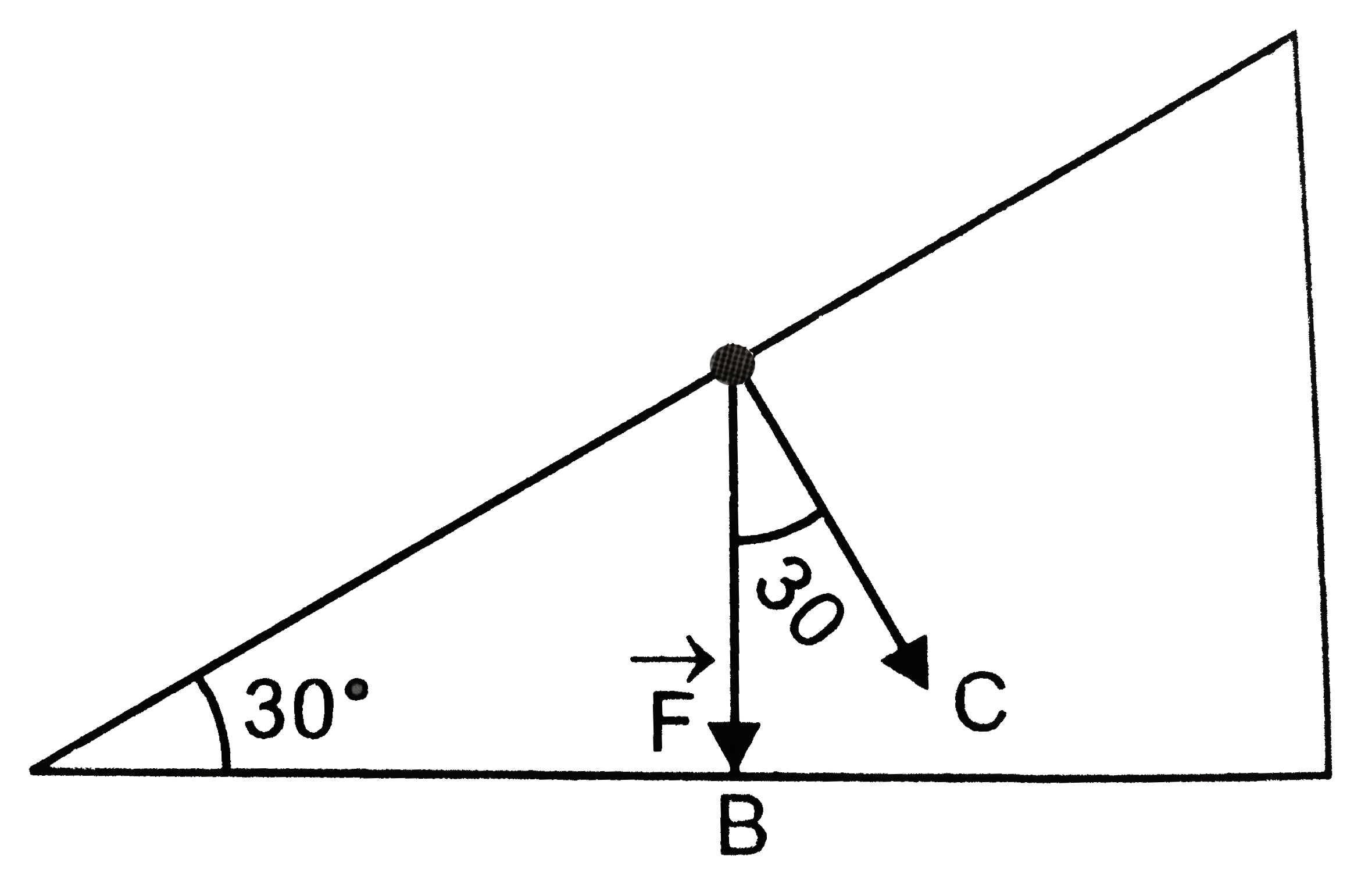
A plane is inclened at an angle of 30∘ with horixontal. Find the componet of a force ltbRgt →F=−10ˆkN perpendicular to the plane. Given that z-direction is vertically upwards.
Refer to Fig. 2 (c ). 93, it is gven that the Z-direction is vertically upwards. Therefore, the force ltbRgt veF=−10ˆkN must be acting vertically downwards, i.e. along AB, The component of →F perpendicular to the plance, i.e. along AC, is
10cos302=10×√3/2=5√3N
 .
.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 Problems for practice45videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Multiple choice10videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 Problems for practice36videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A plane is inclined at an angle 30∘ with horizontal. The component of a vector →A=−10k perpendicular to this plane is: (here z-direction is vertically upwards)
A5√2B5√3C5D2.5
Let θ be the angle between two vectors →A and →B and ˆn is a unit vector perpendicular to their plane.
 View Solution
View SolutionFind the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane →r.(ˆi+2ˆj−5ˆk)+9=0.
View SolutionFind the direction cosines of the unit vector perpendicular to the plane →r.(6ˆi−3ˆj−2ˆk)+1=0 passing through the origin.
View SolutionFind the direction cosines of the unit vector perpendicular to the plane →→r⋅(6ˆi−3ˆj−2ˆk)+1=0passing through the origin.
View SolutionFind all vectors of magnitude 10√3 that are perpendicular to the plane ˆi+2ˆj+ˆk and−ˆi+3ˆj+4ˆk.
View SolutionFind the direction cosines of perpendicular from the origin to the plane →r.2ˆi−3ˆj−6ˆk+5=0.
View SolutionFind the vector equation of plane passing through the points 2ˆi+ˆj−ˆkand−ˆi+3ˆj+4ˆk and perpendicular to the plane →r.(ˆi−2ˆj+4ˆk)=10
View Solution

